Frequency decoders [Advanced Radio Control (1965)]

The element of the control system following the receiver is the decoder. Our interest now lies in frequency decoders and their possible application to simultaneous and proportional control. Frequency de coders use tones (or variations of tones) to convey the control signals.

The reed type decoder has achieved great popularity among radio control enthusiasts. This decoder is used to operate relays which, in turn, activate the various control mechanisms that use either no power or full power. We are going to assume that you are familiar with this operation and we will cover other possible applications of this unit.

The problem

Fig. 301. Triple reed decoder responds to three audio tones. One basic problem in adapting the reed-type decoder (Fig. 301) to simultaneous-proportional control is the fact that it is essentially an OFF-ON device. When the reed vibrates it makes intermittent contact with a fixed point.

Auxiliary relay

The intermittent reed contact is undesirable in most switching applications. An auxiliary relay is used to give a steady closed contact whenever that relay reed is vibrating.

An auxiliary-relay circuit for use with the reed relay is shown in Fig. 302. Here the auxiliary-relay coil is represented by an inductance...

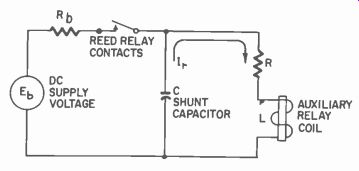
Fig. 302. Auxiliary relay circuit.

...(L) in series with a resistance (R ). The capacitor (C) connected across the coil is used to store energy during the closed period of the reed-relay contacts and then discharges this energy into the coil of the auxiliary relay during the reed open-contact period.

The reed-relay contacts operate at a frequency (f) and are open for as much as 95% of each cycle so that the length of the open period is very nearly equal to 1/f. The closed period is not less than 120f.

For intermittent duty at frequencies greater than 200 hz, the auxiliary relay coil may have a resistance of 5,000 ohms and require as much as 200 milliwatts to operate. The inductance of the relay coil should be around 12 henries, the supply voltage (Eb) should be 3.5 times the maximum required to pull in the relay armature (Eb = 3.5 X I rit ) and C = .5 µf. Where operation is to be more frequent or where extra long life of reed contacts is desired more sensitive auxiliary relays must be used.

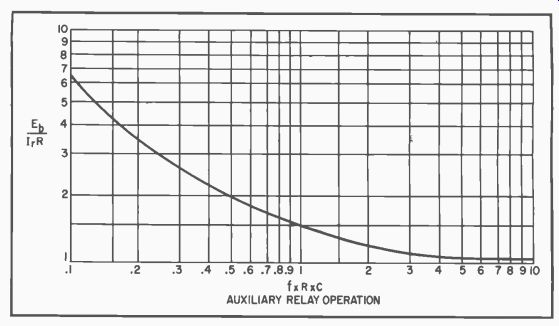
Fig. 303. Curve to determine auxiliary relay shunt capacitance

Fig. 303 shows a curve from which the value of the shunt capacitance (C) can be determined for any desired supply voltage. The supply voltage must, of course, exceed the pull-in voltage of the relay.

To use the curve, determine the value of:

Eb / I rR

from the required supply voltage. Next, determine a value of f X R X C and the value of the capacitor (C) from this. Make an allowance in either Eb or C to insure reliable operation, then compute the charging resistance (Rb) from

0.012 Rb f X C

Check the computation by determining the peak current through e.

the reed contacts and voltage across these contacts. These should not exceed 0.75 ampere and 200 volts. Note that if f X R X C is greater than 0.5, the value of Eb may be taken as the contact voltage. As f X R X C becomes smaller than 0.5, the contact voltage approaches 2 Eb.

Part of this basic problem is to make just one reed vibrate at a time in response to a control signal. This is due, in part, to our inability to transmit and receive absolutely pure and stable tones. Normally the wave shapes are distorted, either in the tone generator, transmitter, or receiver and they contain harmonics or secondary frequencies which cause a reed other than the desired one to vibrate.

Considerations for proportional control

By examining the reed operation curve (Fig. 304) more closely, it is possible that some facts concerning this unit may lead to some new applications.

To achieve proportional control, we are limited to changing the amplitude of vibration and the frequency of vibration. Amplitude of reed vibration can be controlled by governing the amount of power or by the frequency sent to the reed coil.

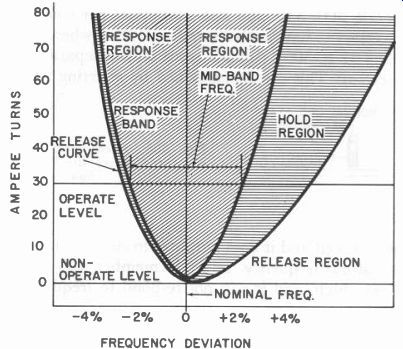
Fig. 304. Reed relay response characteristics.

Fig. 305. Commercial frequency meter has reeds which respond to frequencies which are very close to each other. [ James G. Biddle Co.]

Try to visualize the amplitude of a reed's vibration as varying between extremes in a gradual manner as it responds to a tone just below, exactly at and just above the reed's resonant frequency. Note that in many radio-control reed decoders, frequency separations of about 30 cycles are required between reeds. The frequencies generally used are 240, 270, 300, 330, 360 and 390 cycles per second.

Why is it necessary to have such a large separation when commercial frequency meters (Fig. 305) can use reeds with a separation of only 0.5 cycle per second? This can be explained by referring to Fig. 306.

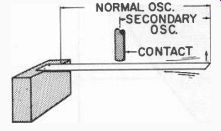
Fig. 306. Reed secondary-vibration concept. Contact also "damps" vibration.

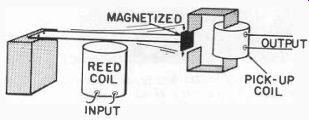
Fig. 307. Using unloaded reed as filter.

If we energize a reed and it does not have to strike a contact, it will oscillate at its natural frequency. Its Q (remember, this is the bandpass) will be very high, and it will not respond to frequencies a few cycles away.

When the reed must strike a contact, two things happen. First, its Q is lowered, and second, at the moment of striking the contact, the effective length of the reed is changed and it vibrates with a secondary oscillation. If you were to connect a reed unit to a precision audio generator tuned exactly to the reed's natural frequency, and were to increase the gain gradually so that the reed started vibrating, you would see the vibration gradually increase in amplitude until the reed hit the contact. As soon as the reed hits this contact, the vibration will diminish and stop. Then it builds up again in the same manner.

This intermittent operation results because the resonant frequency of the reed changes when it strikes the contact.

In practice, this intermittent effect is overcome by adjusting the transmitter tone oscillator so that its frequency is equal to the contact touching frequency of the reed. This is usually close enough to the reed's unloaded frequency so that vibration starts easily and continues to vibrate with maximum effectiveness.

Perhaps, then, one solution to the problem of utilizing the reed unit in proportional control systems is to have a non-contact method of using reed frequency separation abilities that would maintain a very high unloaded Q. One possibility is shown in Fig. 307. A small coil is positioned so that the vibrating end of the reed will affect its magnetic circuit, producing an alternating voltage proportional in strength to the amplitude of the swing of the end of the reed. This alternating voltage can then be rectified and used to control other mechanisms.

There is no loading on the reed and the Q remains high. The voltage produced will be proportional to the closeness of the transmitted tone to the reed frequency.

Fig. 308. Mechanical control-system decoder uses air pressure.

Reed decoded pneumatic control

Control system decoders using air pressure (see Fig 308) are a little different from those of the more familiar electrical control systems. Connections are by flexible rubber hose or tubing which is not so likely to break, under continuous vibration, as wires so often do.

The system (Fig. 309) works as follows: A vacuum pump, driven by the airplane motor, draws air out of a cylinder, creating a vacuum on one side of a piston, thus causing the piston to be drawn into the cylinder against the tension of a rubber band. The decoder valve manifold housed in the receiver connects to the cylinder, and the vacuum in the cylinder is applied to the manifold. From tiny valves in the manifold, flexible tubes connect the manifold to the pneumatic servos (diaphragms) (Fig. 310) on the control mechanisms. The valves are operated by reeds and relays. When open, each valve applies the vacuum in the manifold to one side of its servo or diaphragm, causing the diaphragm to move and operating its control mechanism. When the valve is shut, atmospheric pressure restores the diaphragm to its original position.

If the vacuum pump fails (let's say the motor stops), a check valve prevents air from flowing to the cylinder. The rubber band will move ...

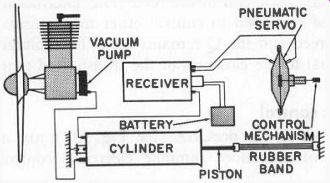
Fig. 309. Pneumatic servo used as a control mechanism.

Fig. 310. Pneumatic servo.

...the piston to pull enough vacuum in the cylinder for returning the model to the operator.

Fig. 311 illustrates another concept which might be appropriate for proportional control. In Fig. 311-a, the reed unit itself is made into a manifold for controlling air pressure or vacuum. Note that (in the small circle) the amplitude of vibration of the reed itself determines how much of the exhaust port is uncovered.

In this method, then, by transmitting a signal a little above or below the actual reed frequency, one can cause the reed to vibrate a small amount. The port would be uncovered a small amount and thus the pressure (or vacuum) to the servo would be small. The result would be a proportional deflection of the fin.

If the signal were exactly at the reed frequency, the maximum vibration would take place, giving full differential pressure and thus maximum control deflection. Fig. 311-b shows how this system is employed to control a model aircraft.

Fig. 311. Proportional simultaneous reed-controlled pneumatic system. The reeds are only a few cycles apart.

The vacuum system has some difficulties, especially when operating aircraft at different altitudes. The atmospheric pressure changes and thus the amount of control surface deflection can vary. If a pressure system were used, that is, if we were to let the pump create pressure, this difficulty might be overcome.

Step-type proportional control--reed decoder

Another method for obtaining simultaneous and proportional control with a reed relay would be to use an electrical bridge which would feed a transistor-amplifier servo system. The input transistor would require very little power. Thus, the reed contact might be light enough and of a type which would prevent loading. The idea is diagrammed in Fig. 312.

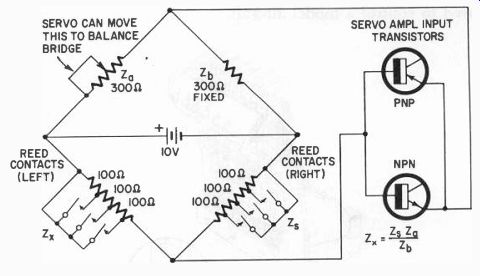
Fig. 312. Reeds can unbalance bridge to give "step" control. The reeds are 3 to 4 cycles apart. The values of the resistors can be increased, if desired.

For multichannel operation a small frequency separation should be arranged between reeds so that there can be at least six reeds per transmitter channel. Assuming a two-cycle separation, and multi channel operation, eighteen reeds would occupy a frequency span of probably 26 to 40 cycles, about the same as used for one channel at present.

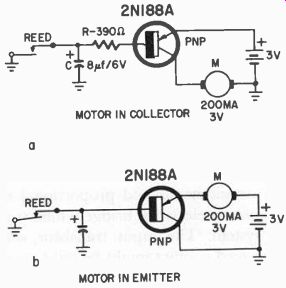
Fig. 313-a,-b. Motor in the collector [a] and motor in the emitter [b].

Circuit operation

When no tone is transmitted, the bridge is balanced and the servo is neutral. Moving the control stick a small amount sends out the first tone which shorts part of one bridge resistor. Because of this unbalance, a voltage is fed to the transistor servo amplifier causing the servo to operate. As the servo moves, it adjusts a potentiometer in the opposite bridge arm to reestablish the balance. The servo stops and the control surface is deflected a small amount.

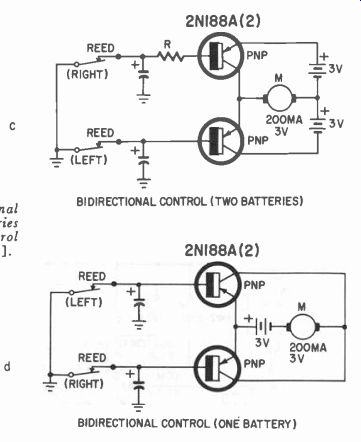
Fig. 313-c,-d. Bidirectional control using two batteries [c] and bidirectional control using only one battery.

Moving the control stick further causes a different tone to be transmitted, shorting more of the bridge resistor. Again the servo, in moving, establishes the balance; the control surface moves a greater amount. When the tone signals to the reed relay stop (neutral joystick position, or loss of signal), the servo-controlled potentiometer, being unbalanced with respect to the other resistances, develops the necessary unbalance voltage to cause self-neutralization. This would be a fail-safe feature.

This is a proven system. It is fail-safe and would give some proportional and simultaneous control, although the proportional aspect would be in steps instead of a completely smooth variable transition.

Fig. 313 gives some of the possible methods of connecting a relay reed, through a transistor, to a servo motor. There will be more on the servo system later.

Transistors are used to replace relays as well as tubes. Fig. 314 shows the circuit for one system. With proper feedback provided, this ...

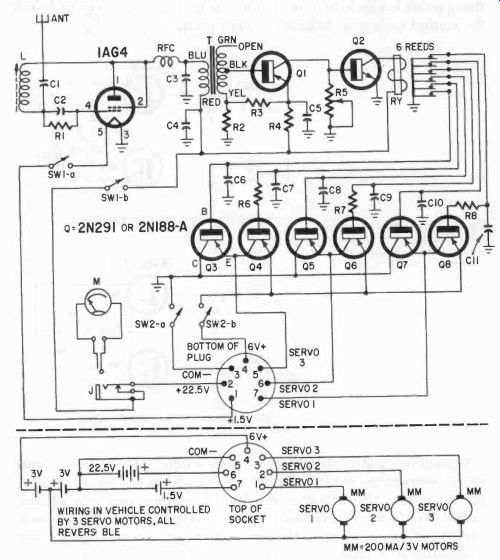
Fig. 314. Complete reed-and-transistor-controlled servo radio-control unit.

... circuit would form the basis for a discrete-step simultaneous proportional system.

Commutating tones and reed decoder for simultaneous control

Another concept in the quest for simultaneous control systems is that of commutating tones. Consider six tone generators feeding the contacts of a commutating switch. As the arm rotates it passes on each tone, in turn, to the transmitter modulator. If the commutation speed is high, an almost simultaneous transmission takes place and the full modulation (100%) is effective on each tone.

Remember that it takes an instant for a reed to build up to maximum vibration amplitude, and an instant for it to die down once excited. We take advantage of this latter fact. We depress one, two or all control switches. The commutator takes care of sending out the tones, whatever their number. The individual reeds vibrate and keep vibrating due to their own kinetic energy, even though the excitations are but impulses. The impulses are, of course, repeated frequently ...

Fig. 315. Resonant-reed [tuning-fork] generator control for use in tone generator circuit. [James G. Biddle Co.]

... because of the rapidity of commutation. Effectively, full tone energy is present in the reed coil at any instant.

It is interesting to note that through the ability to select any combination of six (or more) tones, and therefore any combination of six relays operated by the six reeds, up to 64 individual control functions can be accomplished.

The tone generation problem

We cannot leave the concept of reed units as frequency decoders without mentioning the tone-generation problem. We have indicated the many possibilities for use of this decoder provided we can obtain narrower separations of the reeds. We must remember that with closer reed frequencies we will require more precise control over the generated tones. These must be purer than those currently used.

Tone wheels might be used where the speed of the wheel directly governs the frequency and thus allows precision control by regulating motor speed. Pulse generating circuits make a precise number of cycles per second which can be filtered and smoothed into pure sine waves. Whether tuned circuits, tuning forks or any other mechanical …

-------------------

Capacitors: C1-.1 400 v; C2-part of TF1; C3-.05 id, 400 v; C4-2 pf metallized (paper), 200 v (all :1=20%) Resistors: R1-1 megohm, ± 10%, V2 watt; R2-270K, ± 10%, 1 watt; R3-250K, locking type potentiometer; R4-750 ohms, ±5%, 2 watts; R5-270K, ± 10%, 1/2 watt; R6-3.3 megohm,± 10%, 1/2 watt Tube: Q1-12AU7, 5814-A, 5814-WA or 6189 Tone source: TF1-Frahm oscillator control, ROC unit (frequency as required) Miscellaneous: E1-terminal strip (Cinch-Jones 6-141-Y or equivalent); tube socket, 9-pin (shield type) mica-filled (Elco ST 169 or equivalent); tube shield, 9-pin, 1-15/16 inches high, ventilated (Elco 190V or equivalent); phenolic panel, 3 x 6-3/4 x 3/16 inches; hardware

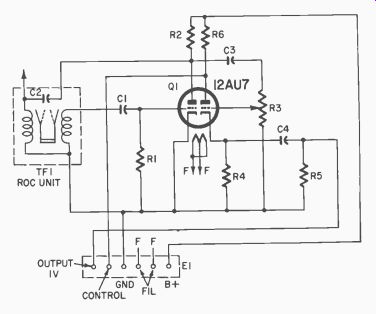
Fig. 316. Tone generator using tuning-fork reed control.

----------------------

… method is used, remember that the tones must be pure, exact, variable, and should not be harmonically related. Since each reed has a definite bandwidth the tones should not overlap bandwidths. Fig. 315 shows a cutaway of one plug-in tone-generator stabilization device, and Fig. ...

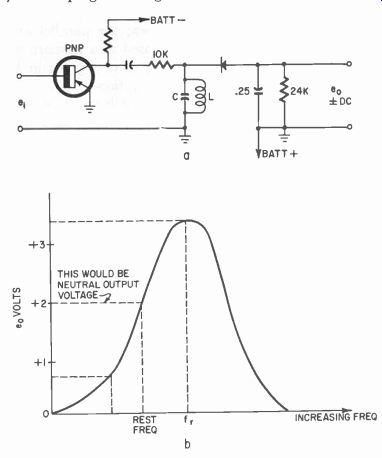
Fig. 317. Slope detector gives only positive or negative voltage output--not both.

...316 shows a circuit for this unit to produce the tones desired. Circuits for transistors are also used.

Discriminators and filters

Since one goal is to be able to control all functions simultaneously and because the reed type frequency decoder is limited in this respect, let's examine some other methods of obtaining proportional control.

Perhaps, next to the reed decoder, the filter-discriminator decoder is most important. Here we transmit several tones at one time, using a filter which separates the tones. Each tone is then converted into a dc control voltage through a slope detector or a discriminator. In some applications the filters may be a separate section of the circuit; in others the frequency selectivity characteristic of the discriminator itself will serve to produce the filter effect.

At the present time, the filter most commonly used to effect tone separation is the simple series or parallel L-C type. Series types are more commonly used with vacuum tubes; the parallel arrangement with transistors. This L-C filter can be used as a proportional control decoder by operating it in a circuit such as that given in Fig. 317-a.

The curve of Fig. 317-b illustrates the operation.

If the transmitted tone is adjusted so that it coincides with the rest frequency, the voltage output eo will be more than minimum and less than the maximum obtainable. The output on the graph indicates...

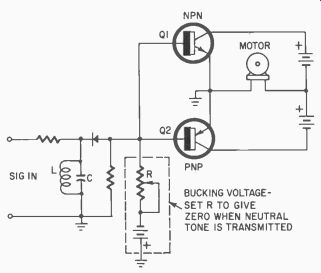
Fig. 318. Modification of slope discriminator.

... plus 2 volts. If the tone frequency is increased, up to fr (the resonant frequency of the tuned circuit), the voltage output increases to about 3 1/2 volts. Lowering the frequency below the rest value will reduce the voltage output to about 1 volt assuming that we want to operate on the more linear part of the curve. The voltage output, eo, varies with frequency and thus becomes suitable for proportional control but note that it does not change polarity. The next problem then is how to get plus, zero and minus voltages using this type circuit.

Furnishing, within the decoder, a circuit which will provide a reference voltage ( which would oppose the output of the slope detector) will produce the desired plus, zero and minus voltage outputs. Refer to Fig. 318. Here, the value of resistor R is adjusted so that the voltage at the bases of the two transistors is zero when the rest frequency voltage is produced by the detector. When the output voltage increases, due to an increase in tone frequency, this plus voltage is greater than the reference negative voltage and thus a plus voltage is applied to the bases of Q1 and Q2. The n-p-n transistor will conduct and drive a servo motor in one direction.

When the signal frequency is decreased, the reference voltage is now the greater and thus the sum of the two will be negative. Now transistor Q2 conducts a current in the opposite direction through the...

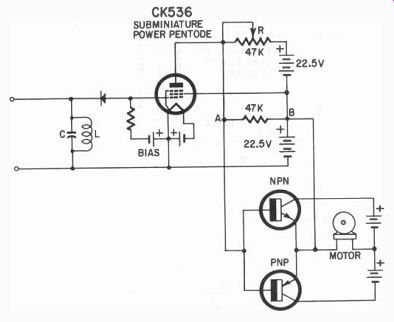
Fig. 319. Using a tube with a tuned circuit gives discriminator action. Adjust R for zero voltage between A and B when "rest" frequency is transmitted.

... motor in its output. This is the desired condition. We have a complete discriminator action using one tuned circuit in a simple arrangement.

A word of caution about using an opposition voltage such as this.

Unless this voltage can be obtained from the signal itself, the loss of a signal would result in only this opposition voltage being present. This would mean a full deflection of a control surface and possible disaster.

This type of control would be most suitable in a controlling device where signal loss would not mean a crash.

Fig. 319 shows how this same idea can be applied to a vacuum tube. In this circuit the tube bias will have to be adjusted to set the tube current at half its maximum class-A value. A variable resistor in the grid circuit will not work since the grid draws no current.

An opposition voltage derived from the signal itself is used in the circuit in Fig. 320-a. Here one diode (D1) rectifies the signal directly and it is balanced against the signal produced from the diode (D2) connected to the tuned circuit. One half of the circuit thus is frequency selective, the other is not.

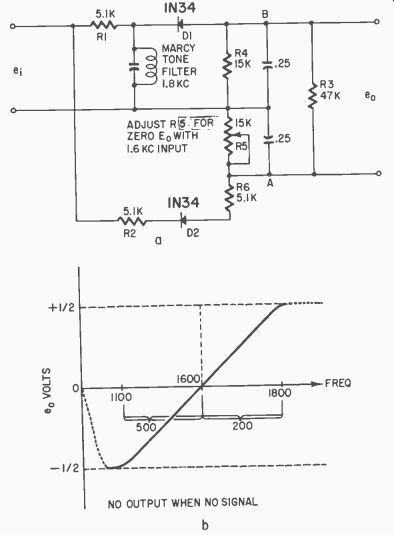
Fig. 320. Discriminator using bucking voltage derived from signal. Adjust R5 for zero output voltage [eu] with 1600-cycle input. The curve shows that there is no output when there is no signal.

In this circuit, R1 and R2 are simply isolation resistors and have the values shown. The diodes must be connected so that the cathodes are in the same direction. R5 and R6 allow proportioning of the non-frequency-selective voltage to the correct value to balance against that produced across R4. The two capacitors and the common load resistor (R3) allow the balancing action to take place.

A tone from an audio generator is fed into the input as ei. A high resistance voltmeter (20,000 ohms/volt or a vacuum-tube type) set to about a 10-volt scale can now be connected across R4. The audio generator is adjusted to give a maximum reading. Next the audio generator is tuned carefully away from this frequency to a new frequency where the voltage across R4 is just zero. Now the meter is connected across R5 and its value is adjusted to give a reading at least 3/4 the value obtained across R4 when the generator is tuned to resonance with the tuned circuit. Finally, the meter is connected across the load, points A and B. The generator is retuned toward the frequency which gave a maximum across the tuned circuit. At some value the voltage will be zero. Now the generator dial is moved first higher and then lower in frequency and R5 is adjusted until a good linear plus and minus swing is obtained. An indication of the results obtained in one test using a filter tuned to 1,600 cps is shown in the graph of Fig. 320-b.

The difficulty with this kind of circuit is that since only one branch is frequency selective, it normally would be suitable for only one proportional control function. One could not obtain multichannel proportional control without adding another frequency selective element in the R1--R4 side of the circuit or preceding this circuit with a band pass filter. This circuit however, is fail safe. In the event of signal loss there is no output and therefore the servo will return to a neutral position.

Fig 321. Slope detector using split capacitor output.

Another type of slope detector is shown in Fig. 321. This detector, although connected somewhat differently, produces about the same effect as those previously described.

R-C type discriminators

In an effort to obtain a discriminator which could be as small as possible, the concept of using an R-C (resistance-capacitance) network to produce the positive and negative output voltages needed for proportional control was investigated. The theory was simply that at the rest frequency the capacitive reactance of a capacitor could be made equal to that of a resistor in a bridge circuit. As the frequency would decrease, the reactance would increase, unbalancing the bridge in one direction, and as the frequency increased the capacitive reactance would decrease, unbalancing the bridge in the opposite direction. A ...

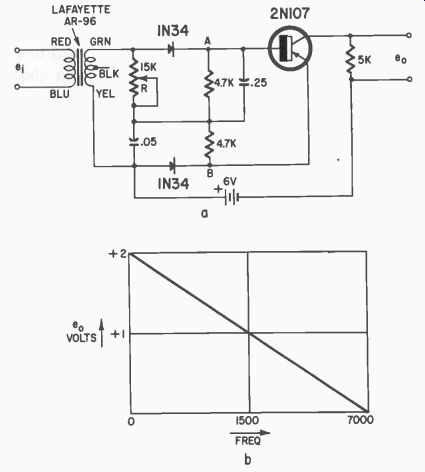
Fig. 322. R-C discriminator. Set R to zero with input signal at "rest" frequency. At 3,000 cycles, the voltage across A-B is zero. It increases to +1 volt at 9,000 cycles and becomes-1 volt at 1,000. Signal loss gives zero output.

... transformer was used to feed the network to provide isolation from the source. The circuit is shown in Fig. 322-a. Fig. 322-b shows the test results with the values specified.

The output of this circuit was so low that a transistor had to be used as a driver for the servo amplifier. Note also that R is variable. This could be a feedback potentiometer which is driven by the servo motor to reestablish bridge balance.

In general, the response was quite broad, as shown in Fig. 322-b and indicated that if more voltage amplifying stages were used, the operating band of frequencies could be reduced, as is necessary for multichannel control.

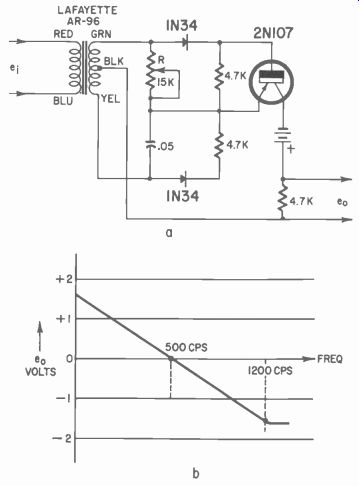
Fig. 323. Amplitude and frequency discriminator. Set R for zero output voltage [b] at 500 cycles.

The circuit in Fig. 323-a is also an amplitude detector producing a plus or minus output by varying the amplitude of the input signal. It still retains the ability to produce control signals with frequency variations as shown in the graph of Fig. 323-b, when the amplitude is adjusted to a given value.

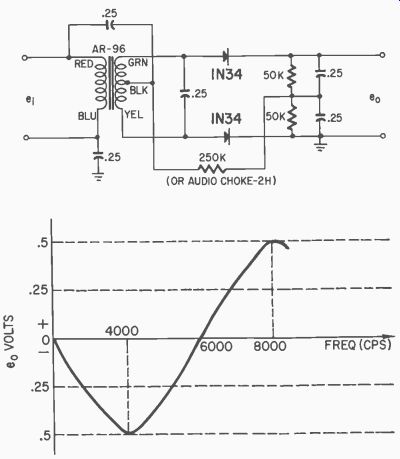
Fig. 324. Foster-Seeley type discriminator. Signal loss gives zero output. Large input signal is required. Performance may be improved with high Q transformer.

Balanced (Foster-Seeley) type discriminators

A Foster-Seeley type discriminator was used at audio frequencies.

The circuit is shown in Fig. 324. Although a relatively low Q transformer is used, discriminator action was obtained but with relatively low output voltage. There is no output unless a high driving signal is used. However, by using a high Q transformer and varying the circuit values, it may result in a discriminator adequate for radio-control purposes.

Two tuned transformers have been used to obtain a discriminator suitable for simultaneous proportional radio control. This circuit is shown in Fig. 325-a. Note that this is a complete one-channel system.

Fig. 325-b shows how, through stagger tuning of the two transformers, one is able to produce different voltage maximums at different frequencies. When the rectified output of L3 is negative to that of L4 the discriminator curve of Fig. 325-c is obtained.

L1-15 turns No. 28 enameled wire on CTC PLS 6-2C4 LD coil form L2-1,200 turns No. 38 enameled wire on Arnold Engineering Co. A050056-2 toroid form L3, L4-primary, 300 turns No. 32 enameled wire on A050056-2 toroid form L3, L4-secondary, 350 turns No. 38 enameled wire wound over primary

Resistors-all 1/2 watt

Capacitors-3, 5 and 15 uuf are silver mica

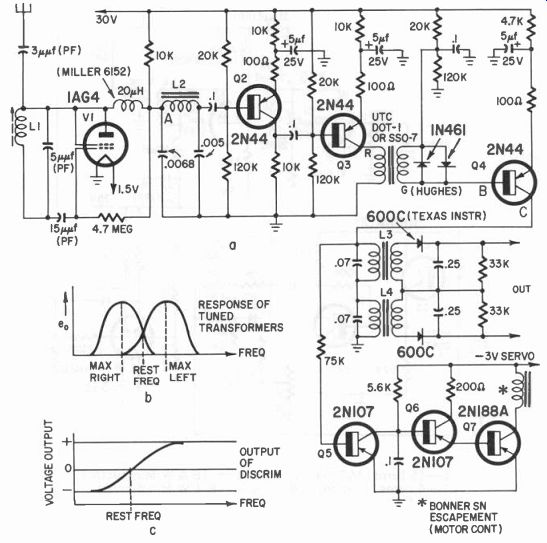
Fig. 325. Receiver for complete proportional-control R-C system. This is a single-channel receiver for 50 mhz.

To obtain a discriminator which would produce the plus, zero and minus output voltages for the narrowest range of frequencies using commercial filters, the circuit of Fig. 326-a was constructed. Two identical 1,800 cycle filters were modified to retune them to 1,550 and 2,000 cycles. To decrease the frequency an additional capacitor of .1 1,11 was added across one unit.

L1-15 turns, 1/2" diam., 10 turns/in. [B & W Miniductor]

L2-4 turns, 1" diam., 10 turns/in. [B & W Miniductor]

L3-2-turn loop

Resistors-all 1/2 watt

Capacitors-C1, 50 AO, Hammarlund MAPC-50

C2, 35 AO, Hammarlund MAPC-35

Fig. 325 [continued]. 50 me proportional-control transmitter.

The second unit was carefully opened so that all of the bright wire wrapping could be removed. We reduced the number of turns down to the black wire which is the standard winding for these filters. The only requirement was to increase the resonant frequency of this second filter about 500 cycles above the first. One might slide out the core to do this if the proper glue-softening agent is used.

This circuit gives excellent discriminator action (Fig. 326-b) and is nonresponsive to frequencies below 1,000 cycles and above 2,500 cycles. This means that similar discriminators could be used if their resting frequencies were about 500, 4,000 and 8,000 or 9,000 cycles.

Three such discriminators could operate with sufficient separation between them so that no crosstalk or "spillover" would occur.

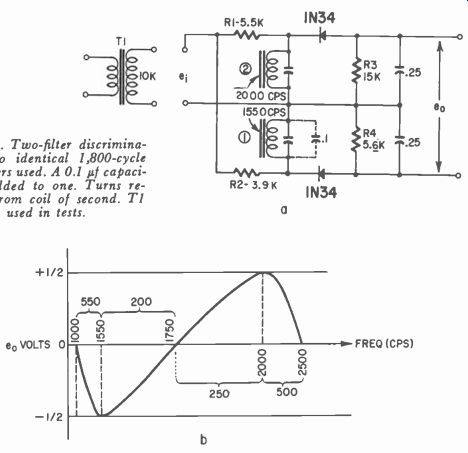
Fig. 326. Two-filter discriminator. Two identical 1,800-cycle tone filters used. A 0.1 µf capacitor is added to one. Turns re moved from coil of second. T1 used in tests.

Fig. 327. Symmetrical transistor discriminator. Transformer T must be a high-Q unit.

Fig. 328. Ratio detector might be used for proportional control. T would have to be an audio trans former having high Q and a third winding. R2 and C, de-emphasis network for FM receiver use, can be omitted. Output signal is developed across R1.

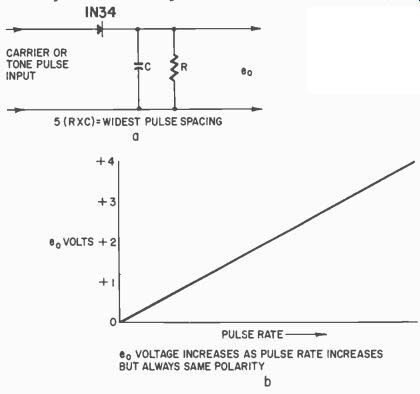
Fig. 329. Detector circuit [a] converts varying pulse rate to a varying dc voltage proportional to the rate [b].

The values of R2 and R3 are adjusted to balance the output to zero and give good linearity. One might use variable resistances here, adjust them for proper response, then replace with fixed values. The resistance values used at R3 and R4 were just arbitrary selections as to range.

One might use much higher values as long as R3 is made adjustable to obtain the balance and linearity required.

Two other detector circuits which can be adapted to the proportional control problem are given in Figs. 327 and 328. Although both employ transformers, there is difficulty in getting transformers small enough to make their use feasible. High Q transformers will produce the best results, and in both cases the transformers must be capable of being tuned to the desired frequency, as was done in the circuit in Fig. 326.

It is possible to use pulse rates instead of tones, particularly with single-channel equipment. The detector circuit of Fig. 329-a will convert a varying pulse rate into a dc voltage that is proportional to the rate ( Fig. 329-b).

Although it gives only a unidirectional voltage change, this can be used to operate another circuit which, in turn, will convert it to the necessary plus and minus voltages to drive the servo amplifier. Fig. 330 illustrates one such circuit. This is basically a bridge, circuit with a transistor connected in one leg. A variation in the impedance of the...

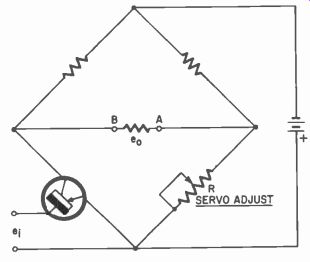
Fig. 330. An increase or decrease of et can give a plus or minus polarity of e, at A with respect to B.

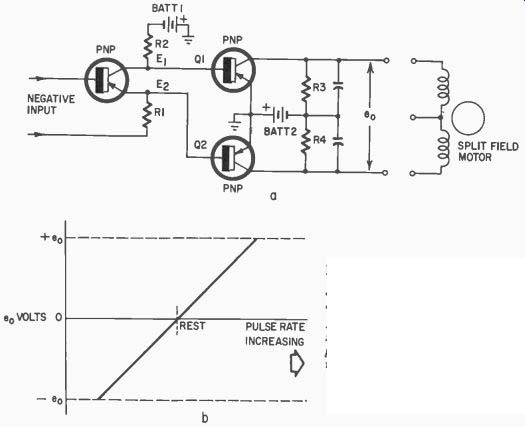
Fig. 331. Adjust R1 and R2 [drawing a] so E1 = E2 when "rest" pulse rate is input or "rest" dc level voltage is input. R3 and R4 are adjusted to give zero output when E1 = E2. The graph [b] shows a plus and minus output from a single-polarity input.

...transistor (either higher or lower than R) will cause a polarity change between points A and B. These points in turn are connected to the bases of a complementary-symmetry transistor servo amplifier.

The servo motor can be made to vary resistance R in such a direction as to rebalance the bridge whenever the transistor voltage input et causes an unbalance in its leg. Proportional control is thus achieved.

Another method of using the output of a detector such as that in Fig. 329-a would be to feed the amplifier circuit in Fig. 331-a. In this case, the input transistor would have a negative input by having the correct polarity from the diode circuit of Fig. 329. With the rest pulse rate being transmitted, the voltages E1 and E2 from the input transistor are adjusted for equal voltage drop values by varying R1 and R2.

Since ground is positive ( battery B1 having its plus terminal connected to ground), the voltages at the collector and emitter of the first transistor would be negative with respect to ground. This would cause Q1 and Q2 to conduct. Assuming that both transistors are identical ( and if they are not, then R1 and R2 could be adjusted so that they do conduct an equal amount) the voltage drops across R3 and R4 would be equal and ea would be zero. The graph in Fig. 331-b shows how eo might vary as the pulse rate was changed to a higher or lower value than the resting rate. This voltage then could be used to drive a servo amplifier as previously mentioned. The use of a split field winding motor instead of R3 and R4 is another possibility. The circuit could drive a motor directly provided its current is low enough.

A disadvantage of this circuit is that, in the event of the loss of the control signal, the circuit would unbalance and cause a full deflection of the control surface. To prevent this a fail-safe relay might be incorporated. This relay is so wired into the circuit that if the pulse rate or input voltage drops below a certain value, the relay contacts (Fig. 332) would break the circuit to the servo amplifier input. The servo amplifier would then neutralize; this degree of neutralization would have been previously set by the adjustment of R.

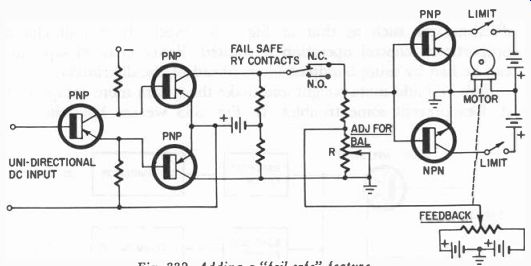
Fig. 332. Adding a "fail-safe" feature.

Fig. 333. Separation of audio spectrum into bands for proportional control.

There are many ways in which the relay contacts can be made to remain open or closed as long as there is a pulse rate existing in a circuit. The basic idea is to feed the input signal to a second transistor amplifier which, for example, would conduct as long as the pulses were present and stop conducting when the pulses stopped or the rate became too slow to hold the relay contacts closed. In this case, the relay shown in Fig. 332 would have circuit continuity through its armature and normally open contact instead of as shown.

Narrowing the bandpass

There are many circuits which convert a change in the audio tone or pulse rate into a plus or minus control voltage, depending upon whether the tone, or pulse rate, increases or decreases from the resting frequency. The next problem, then, is to consider how to achieve better channel separation especially when using the R-C type separator in which only one component of the circuit is frequency sensitive.

Better channel separation is useful even when using a relatively narrow discriminator such as that in Fig. 326, especially if multichannel proportional control operation is wanted. Better channel separation can be had by using bandpass filters ahead of the discriminators.

This will add more weight and make the system more complex, but it does prevent some troubles. In Fig. 333 we see how the audio...

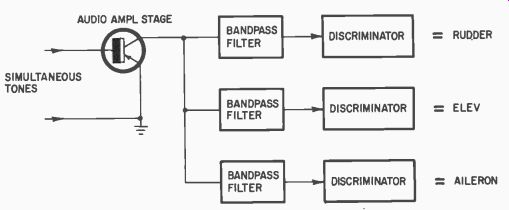
Fig. 334. Band pass filters are used in front of discriminator.

...spectrum may be split into band 1, band 2 and band 3 by means of filters. The signal from the filters is fed to the discriminators ( Fig. 334 ) ...

Fig. 335. Compact band pass filter.

... to prevent spillover trouble that is found when operating a multi channel proportional control system.

A bandpass filter is shown in Fig. 335. Note its size as compared to the 25-cent piece. The frequency of this particular one is 7.5 khz. By using special coils, lower frequency filters but slightly larger in size are available. Fig. 336 shows an electromechanical type of bandpass filter which can also be used.

Circuits and components

Having established a need for such devices, let us now turn our attention to some of the circuitry, components and calculations involved when using bandpass filters.

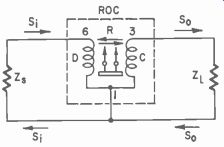
Fig. 336. Electromechanical bandpass filter. [Z., signal source impedance; ZL, signal load impedance; S1, input signal of resonant frequency; S., out put signal of resonant frequency; ROC, electromechanical bandpass filter; D, signal input coil; C, signal output coil; R, resonant reeds.)

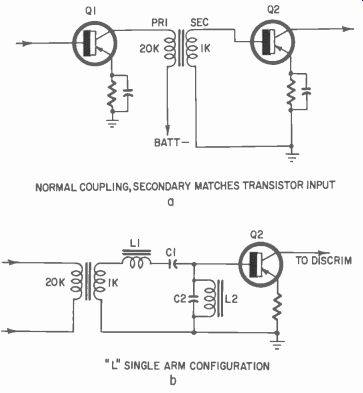
Fig. 337. Interstage transformer provides correct input impedance; transistor correct termination impedance. Typical transformer coupling [a] and single arm "L." configuration [b].

Fig. 337-a shows a basic transformer coupling circuit between two amplifiers. Note that it is necessary to match impedances. The trans former takes care of this impedance matching problem between the collector of the first transistor and the base of the second transistor by providing a 20,000-ohm impedance winding for the collector circuit and a 1,000-ohm impedance winding for the base-emitter circuit.

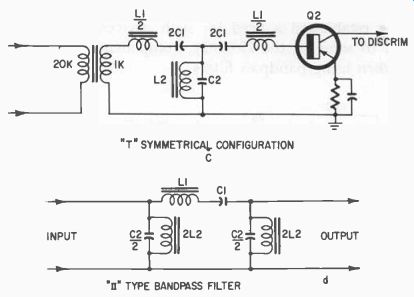
Fig. 337 [continued]. "T" symmetrical configuration [c] and ,r-type bandpass filter [d].

Fig. 337-b shows a basic bandpass filter which is placed between the transformer secondary and the second transistor. In placing it here, the input to the filter is 1,000 ohms and the terminating resistance (the emitter-base impedance) of transistor Q2 is 1,000 ohms. Note also that this bandpass filter consists of a series resonant circuit L1, C1 and a parallel resonant circuit L2, C2. If the series circuit is tuned correctly, it will let the frequencies we desire pass easily and reject those we don't want. The parallel circuit, on the other hand, will present a shunting circuit to the frequencies we don't want and will present a high impedance to those we do want to send on to the transistor Q2.

Filters generally fall into two categories, or perhaps we should say three categories; the L type shown in Fig. 337-b, the T type in Fig. 337-c, and the so called 7 (P1) type in Fig. 337-d. Basically, we design an L section and obtain values for the chokes and capacitors; then we can rearrange the circuit according to Figs. 337-c or d by simply making the values either half or twice those calculated for the L section alone.

The T and r type filters are symmetrical; that is, regardless from which end of the circuit you start at, there are the same value components. This means, in turn, that when we design a symmetrical filter to work into a given impedance, that same impedance will be reflected back through to the input. For example, if the characteristic impedance of a T or pi type filter is 500 ohms, its terminating resistance should be 500 ohms and its input should be 500 ohms. We can cascade additional filter sections to obtain a sharper bandpass. In Fig. 337-c the filter is placed between the 1,000-ohm transformer winding and the transistor base so that input and output impedance of the filter are both 1,000 ohms.

Filter calculations

To determine what values of capacitors and inductors to use to give a certain bandpass (and to match impedances at the same time), use the method of calculation given in Fig. 338.

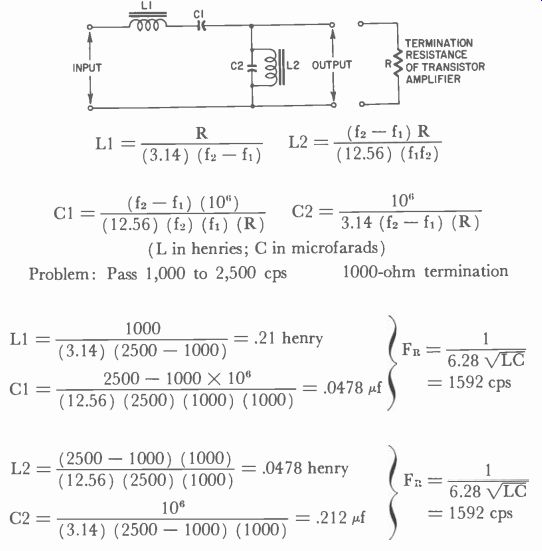
Fig. 338. Bandpass filter calculations.

The lower bandpass limit is f1 and f2 is the upper bandpass limit.

As an example we will use the frequencies of 1,000 hz and 2,500 hz, which will work with the discriminator in Fig. 327. This filter incorporated into the circuit ahead of the discriminator will prevent cross coupling when used in a simultaneous operation multi-tone radio control system. The calculations are straightforward as shown, and can be used for any other band of frequencies that might be desired.

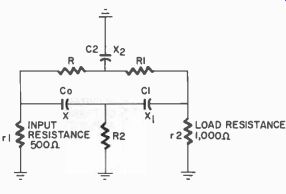
Fig. 339. Twin-T filter showing resistance of source feeding T as 500 ohms and load the T feeds as 1,000 ohms.

Note that we have shown the resonant frequency formula. This was used as a quick check to be sure we did not make a mistake in values.

To solve this equation, insert the values calculated for the L's and C's and obtain a resonant frequency in the bandpass. In this case both were resonant around 1,600 cycles per second.

R-C filters We should not leave the subject of filters without mentioning the most selective of the RC filters- the parallel or Twin-T (Fig. 339)- as another possible solution to the problem of filters.

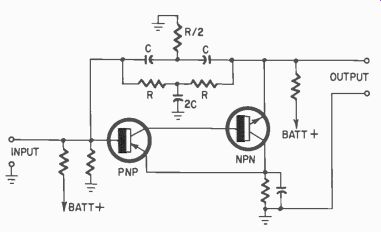
Fig. 340. Method of connecting a Twin-T to obtain a bandpass amplifier.

The Twin-T can be operated as a negative feedback element in either a transistor or tube circuit. Two transistor applications are given ...

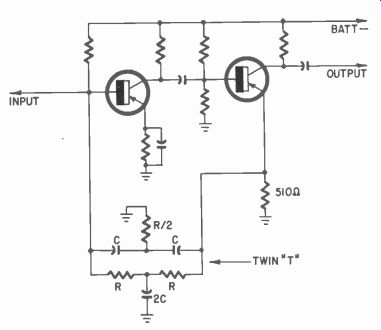
Fig. 341. Another method of connecting a Twin-T to obtain a bandpass amplifier.

...in Figs. 340 and 341. In general the frequency that will be passed with the most amplification using this network is:

1 1 274 = R X C or f = (6.28) RC

For example, let R equal 1 megohm and C equal .005 pi then:

f (6.28) (1 X 106) (.005 X 10') 1 1 (6.28) (.005 )

When the source and load impedances are high, they can be neglected. Low impedances of the transistor circuits cannot be ignored as easily since they affect the bandwidth of the filter.