AMAZON multi-meters discounts AMAZON oscilloscope discounts
When we consider the future of radio control, we must not overlook the rocket as a controlled vehicle. With proper vocational guidance and personal effort, this could well provide the foundation of a career in this exciting field. To the old timer in the radio-control field, this could supply an added stimulus, a new challenge to his abilities and imagination. To anyone interested in the fields of science and space technology, it is hoped that this and the following section will provide greater understanding of space conquering vehicles.
We have to start by learning the basic concepts which will allow us to design and build some model rockets in the sections to follow.
Radio control of rockets
When considering controlled rockets, we must at once readjust our thinking concerning the object that the commands will be sent to. We must modify our thinking in terms of the speed at which these commands must be sent and executed. We must re-evaluate the methods used to keep track of the controlled rocket; that is, its position and its altitude.
A controlled model airplane is easy to watch with just our eyes. We can see if it is flying straight, turning, has one wing high or nosing up, and we can send commands manually to correct these problems. With a rocket the command problem is divided into two parts, both of which must be performed automatically because of the tremendous speeds involved.
Begin your examination of this new type of vehicle by looking at the rocket body. Note in Fig. 601-a that it is symmetrical along its longitudinal (roll) axis and in Fig. 601-b that its fins are placed equidistant around the tail and that, in this example, it does not have wings. Note also that we have defined three axes about which this body can move, or rotate. These axes are the pitch axis, which is an imaginary horizontal line through the center of gravity of the rocket; the yaw axis is an imaginary vertical line through the center of gravity, and the roll axis is the longitudinal axis of the rocket.
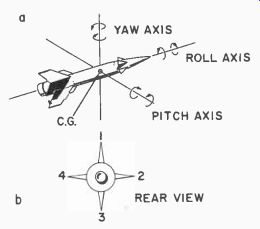
Fig. 601. Rocket axes and fin designation. Here is the first problem in a
rocket. A rocket without automatic controls will spin during the first part
of its flight because of unequal blast-off pressures and other conditions.
It points in the direction it is going because of its fins. However, the operator
has no way of telling which fins are in the rudder position and which fins
are in the elevator position.
How important is this? If we were to designate fins 1 and 3 (Fig. 601-b), say, as rudders, and we planned to send signals to these to make the rocket turn, we might find ourselves sending a signal for left and having the rocket going up. Thus you see that if this symmetrical rocket rolls, we won't know what our command will produce. What is required is a roll-control system built right into the rocket to keep it from rolling, to hold the rudders (1 and 3) in the required vertical position and the elevators (2 and 4) in their proper horizontal position. Then we can send commands and make the rocket go where we wish.
To control the spin (or roll) of a rocket, it is necessary to provide two small control surfaces (Fig. 602) which can be moved differentially, like airplane ailerons, to counteract the roll. In some rockets the regular steering fins are used; in others the rocket jet may be directed to prevent roll, or small auxiliary jets may be provided on the rocket body for this purpose. Whatever method is used, these surfaces (or jets) must be moved by some mechanism, and this mechanism is called the roll-control servomechanism.
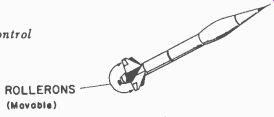
Fig. 602. Roll is controlled by roll-control surfaces.
For this roll-control servomechanism to move the roll-control surfaces in the correct direction, it must be able to tell when the rocket is rolling. Sound funny? Have you ever been up in a plane, or seen pictures from an airplane which show the earth turning? If you were out in space without any nearby object, could you tell whether you were turning or whether the stars and planets were turning instead? We must provide our servomechanism with some means by which it can tell whether the rocket is rolling or not. We can do this with a gyroscope.
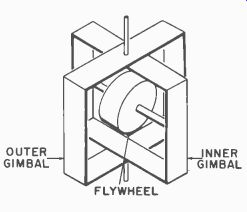
Fig. 603. Gyroscope is a flywheel in a gimbal system.
Perhaps you have had experience with the gyroscope as a toy. Like a top, it stands upright as long as it is spinning. A hoop or an automobile tire will remain erect as long as it is rolling. If you ever had a toy gyroscope you may remember seeing it remain erect as it slid down a string or balanced in your hand. What is peculiar about the gyro scope? Think of this: as long as your gyroscope is spinning it tries to keep its spin axis pointed, say vertical. You can move it around on the palm of your hand but it doesn't tip or fall over--it keeps its axis pointing up.
This phenomenon is known as rigidity in space and is a property possessed by every spinning mass. If we take this gyroscope or flywheel, mount it in a series of rings called gimbals, spin it at a high speed, place it in a missile, it will keep its axis always pointed in the same direction.
This will provide the rocket with a reference so that it can tell when it is rolling, in which direction, and how much. Fig. 603 shows the basic flywheel mounted in its gimbal system. Fig. 604 shows the complicated roll and steering control mechanism of the Nike Hercules (Army).

Fig. 604. Roll and steering-control mechanism of Nike Hercules.
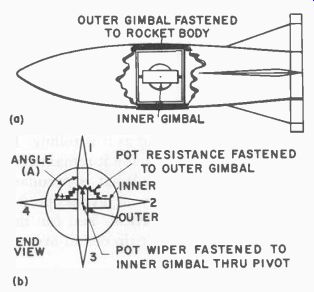
Fig. 605. Gyro mounting in rocket to detect roll.
WIPER NOW OFF CENTER GETS NEG VOLTAGE. NEG VOLTAGE THUS IS LEFT ROLL; AMOUNT OF VOLTAGE PROPORTIONAL TO ROLL ANGLE POLARITY OF VOLTAGE STATES DIRECTION OF ROLL
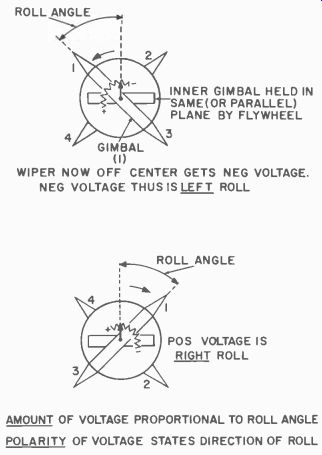
Fig. 606. Potentiometer voltage indicates direction of roll.
The gyroscope can detect the direction and amount of roll and produce a signal which will cause the servomechanism to deflect the roll control surfaces in the proper direction and in the proper amount.
Fig. 605 shows the basic gimbaled flywheel mounted in a rocket missile with the flywheel axis perpendicular to the longitudinal axis of the missile. Fig. 606 shows another view of this same gyroscope. Note that we have added a potentiometer to the gimbal system. The wiper arm of the potentiometer is fastened to the inner gimbal; the resistance portion of the potentiometer is fastened to the outer gimbal. When angle A (see Fig. 605-b) is 90° the wiper is centered on the resistance.
If we move the inner gimbal counterclockwise while the outer gimbal is held in its vertical position by the rocket body the wiper arm will move toward the positive end of the potentiometer resistance. If we turn the inner gimbal clockwise, increasing angle A, the wiper arm will move toward the negative end of the resistance.
When operating in the rocket guidance system, the action is a little different since the inner gimbal is held in a fixed position by the gyroscope while the outer gimbal, fixed to the rocket body, is the one that actually rotates. Thus when the body of the rocket rolls counter-clockwise, the resistance moves, bringing its negative end toward the wiper. If the rocket should roll clockwise, the resistance moves to bring its positive end toward the wiper. When the wiper is at the center of the resistance, it has zero potential. The amount of roll can be measured by how high the voltage is while the polarity of that voltage will indicate/the direction of the roll. A servo system can use this voltage to deflect the fins in a method similar to those in Section 5.
Rocket servos may be electric, pneumatic or electrohydraulic, types powerful enough to move control surfaces against torques as high as 50,000 inch-pounds.
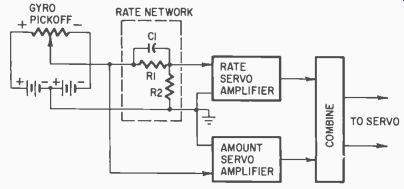
Fig. 607. Simplified diagram of rocket roll-control system. Rate and amount
are combined in proper proportion to prevent roll.
In guidance servo systems the input signal must indicate the amount, direction and rate of roll. The rate is how fast the body is turning. The block diagram of Fig. 607 shows how a simple RC (resistance-capacitance) network can produce a rate signal from the same signal that indicates the amount of roll. These two signals are amplified separately, then combined to control the correcting servo.
Aerodynamics of the rocket
The control problem of guiding a rocket is largely connected with the aerodynamic problem, much as it is in the case of the model airplane. In the rocket, however, we are concerned with much higher speeds, and since the motion is near the speed of sound (about 700 miles per hour), we must also consider such things as the shock waves which can affect the control problem. The shock waves are just one effect; there is another. Because the rocket moves so fast, slight variations (non-symmetry) in the body construction can cause lift and drag forces that are ignored at lower speeds.
The concept of a shock wave is not too difficult. Just imagine that the atmosphere is filled with little molecules of air. When traveling at subsonic speeds a pressure wave or disturbance is set up in the air, like a sound wave. This wave travels ahead of the moving body, warning the molecules of air that the body is coming. The pressure disturbance thus precedes the rocket body.
As speed increases, the body catches up with these pressure disturbances. In fact, when the body is moving at the speed of sound it is moving with the same speed as that of the pressure disturbance.
There can be no warning that the body is coming and the pressure waves tend to build up and remain, like a barrier, at the tip of the rocket.
The wave that is formed is called a shock or mach wave. (The mach number is the ratio: speed of body/speed of sound.) Since the speed of sound is about 700 miles per hour (it varies with tempera ture and barometric pressure), a rocket would be going at mach 1 when it is going 700 miles per hour, mach 2 at 1,400 mph.
Two kinds of pressure waves arc set up around any projection when it is traveling at, or faster than, the speed of sound. These arc the nor mal shock wave and the oblique shock wave as illustrated in Figs. 608 b and-c. There will be an oblique shock wave when the body is moving faster than the speed of sound, and the mach angle of Fig. 608 is indicative of how much faster than that of sound the rocket speed is. The smaller the angle, the greater the speed, etc.
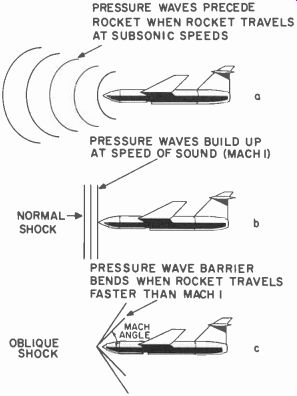
Fig. 608. Concept of a shock wave.
The effect this has on the control problem is that such shock waves will form at the tips of the fins and body. Since they are generally V shaped, they can encompass part of the fin in the shock wave region while leaving the rest outside, as shown in Fig. 609-a. The control forces will be different for the two different regions, and thus we could have instability, and a rocket we could not control.
We desire a fin that is entirely out of the shock-wave region when the rocket is moving at the design speed (Fig. 609-b). This accounts for the many different shapes of fins, which are designed from calculations and experiments to insure that the fins remain outside the shock-wave region.
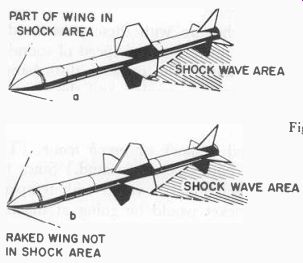
Fig. 609. Effect of shock waves on control.
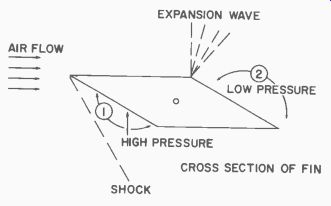
Fig. 610. Shock and expansion waves on fin. Lift is due to high pressure
at 1 and low-pressure region, 2.
The cross-sectional area of a rocket fin differs from that of an air plane. It may be symmetrical and rounded on each side, or it may be diamond-shaped, as shown in Fig. 610. There is also a different concept of lift with the rocket fin. After the airflow passes through the shock wave, its pressure increases, while its velocity decreases.
When the air passes through an expansion wave, its velocity increases and its pressure decreases. Thus, as shown in Fig. 610, there are two primary lift regions on this type of airfoil, sides 1 and 2.
Finally, at the speeds at which the rocket travels, the body itself contributes considerable lift which makes it possible to have just tail surfaces for control and stability. In some rockets jets are used to control direction ( even the rear fins are omitted) and keep the rocket following a stable trajectory.
Guidance systems
There are eight basic guidance systems which have use in the guided missile field today. Five of these are normally associated with surface-to-surface missiles (SSM ) . Here the missile follows a fixed-type trajectory from the launching point to the target. These trajectories may be ballistic or supported, as shown in Fig. 611. In either ...
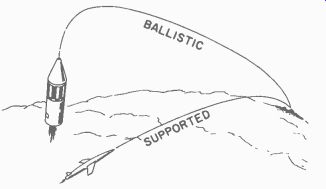
Fig. 611. Surface-to-surface missile [SSM] trajectories.
... case, the path of the missile to the target is set before it is launched.
Then, after takeoff, the position of the missile is adjusted to coincide with this path. Note that for a ballistic trajectory the missile is launched vertically, pitches over towards the target at some fixed angle, continues to climb until the propellants are shut off or used up, and then follows a free-flight ( unpowered ) path to the target. Some ballistic missiles reach a height of 25 to 50 miles, and travel at speeds greater than 3,700 miles per hour. The missile flying a supported trajectory may be launched at any angle from horizontal. It climbs to its operating altitude, then flies at a relatively constant altitude, and dives or glides to impact at the target.
Preset guide
In a preset system, guidance signals are generated in a timed sequence in a device known as a programmer which is mounted in the missile body. This time sequence is set before the missile is launched and cannot be changed once the missile has taken off.
This system is a simple and reliable form of guidance and is used in many missiles today. As the missile is launched, the programmer heads the missile in the general direction of the target and prepares the missile for the midcourse phase of flight. A preset guidance system may also be used when it is desired to test a propulsion system or air frame. In this way, important data on performance may be obtained without the expense of a complicated control system.
A common example of a programmer is that used for an automatic washing machine. It controls the washing of clothes in a predetermined time sequence. The turning of the dial starts a clockwork mechanism that opens and closes contacts within the device in a predetermined manner. This action. controls the washing cycle.
Terrestrial reference (earth reference)
This is a reference system of guidance which uses devices in the missile to detect any change from a course or trajectory.
This type of guidance uses one or more of the properties of the earth and its surrounding medium to compare with preset data to indicate its position along the prescribed path. Some of these phenomena are: atmosphere, magnetic field, electric field, gravitational field and topography. A magnetic compass in the system gives a compass bearing to provide a lateral path control to the target. A small spinning propeller, for example, in the nose of the missile can be calibrated in revolutions per mile and could be a method of range control. An altimeter can be made to indicate when a particular altitude has been reached by the change in atmospheric pressure. The normal variations in each of these indicating elements makes such a system quite inaccurate when used over long distances.
As the basis for a guidance system much work will have to be done before the gravitational field of the earth can be used for missile guidance. The topography of the earth provides a more likely means of guidance. A television camera in the missile might he used to transmit information to a control station or to provide a picture for on-missile comparison to a predetermined course.
Radio navigation
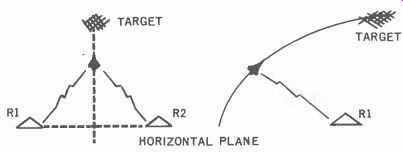
Fig. 612. Radio navigation paths.
Radio navigation as a means of guidance control uses the arrival time of radio signals to determine a position.
The system is similar to the principle used in loran. Radio waves travel at the speed of light. Since this speed is known and the length of time required to send radio signals from one point to another can therefore be measured, the distance between the two points can also be determined. Fig. 612 illustrates two possible courses a missile might follow, using radio navigation for guidance. The missile in Fig. 612-a flies a straight line path by comparing the time of arrival of pulses that arc transmitted simultaneously by radio stations at R1 and R2. If the pulses arrive at the same time, the distance (range) from the missile to R1 will be equal to that from the missile to R2 and the missile will fly along a straight line. In Fig. 612-b the missile transmits pulses to a radio station at R1. As soon as a pulse arrives at R1, it is immediately transmitted back to the missile. The equipment measures the time it takes a pulse to travel to RI and return, and thus measures its distance from R1. The missile then flies a course that keeps this time-interval constant and hence the distance from R1 is kept constant. The path will be an arc.
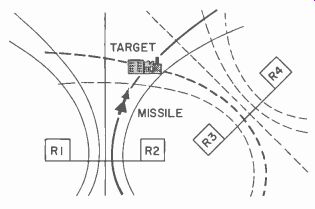
Fig. 613. Hyperbolic radio navigation.
Although radio navigation can indicate circular or straight line courses, it is better to use a hyperbolic path. When a hyperbolic path is followed there will always be a fixed distance farther from one guidance station than from the other. Fig. 613 shows a grid of hyperbolas. The group of hyperbolas indicated by the solid lines is formed by radio stations R1 and R2, and those indicated by the dashed lines by radio stations R3 and R4. A missile flying along the heavy solid-line hyperbola that passes over the target may always be located 1 mile farther from R1 than from R2. The control system computer causes the missile to fly along a hyperbolic path (heavy solid line) by comparing the arrival time of pulses transmitted simultaneously by R1 and R2. Similar equipment uses the pulses being transmitted by R3 and R4 which form another hyperbola (heavy dashed line) that passes through the target. When the relationships between the pulse arrival times indicate that the missile is crossing the heavy dashed line, and hence is over the target, signals are sent to the control surfaces which cause it to pitch over to crash (impact) into the target.
Automatic celestial navigation
Automatic celestial navigation is a guidance system in which navigation is accomplished by making continuous celestial observations.
Such a navigation system aboard a guided missile is similar to that used for marine and aerial navigation. The navigator first positions the telescope of his sextant to establish a line of sight to certain known stars. He then measures the angles of elevation, from a horizontal reference, to these stars. The navigator at sea uses the horizon for his reference; the aerial navigator uses level-indicating bubbles on the sextant to provide an artificial horizon. By using the angles of elevation to two or more stars, the time the observations were made, and information from navigational tables, the navigator can compute his position.
In automatic celestial navigation the same procedure is followed.
Star-tracking telescopes establish a line of sight to known stars. The system must be able to track stars in the daytime as well as at night; otherwise, daytime operation would be impossible. In the missile a stabilized platform provides the horizontal reference required. The computer takes the place of the navigator's brain and the navigation tables. It uses the angles of elevation to the known stars and the time the observations were made to compute the missile position. Knowing the coordinates of the target, the computer continuously sets a course to the target.
Inertial guidance
Inertial guidance is a system that employs accelerometers to measure displacements. It can be used for all phases of guidance in either supported or ballistic missiles. The accelerometer measures the rate of change of velocity. It may be an increase or decrease in velocity.
All movements of the missile result from the application of a force which accelerates the missile. A simple example will illustrate how these measured accelerations may be used for inertial guidance. If the motor of a particular missile provides thrust which accelerates the missile constantly at 100 feet per second, what distance ( displacement) will be covered with this acceleration for a period of 10 seconds? Assuming that the missile started from rest, at the end of 10 seconds, it would have a final velocity, Vt, as follows:
Vf = 100 ft/sec/sec X 10 seconds = 1,000 ft/sec.
Since the missile started from rest the average velocity (Vav) is :
0 + 1,000 Vav 2
= 500 ft/sec.
The distance traveled during the 10 seconds (the displacement) is found by multiplying the average velocity by the time:
S = 500 ft/sec X 10 seconds = 5,000 ft.
Thus, distance traveled, or missile displacement, may be found by knowing the acceleration and the length of time it occurs. Actually, acceleration will not be constant. But the distance may still be found by the mathematical operation known as integration. Devices to ...
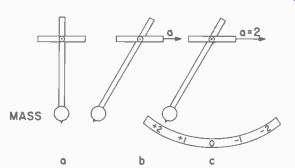
Fig. 614. Accelerometer principle.
... perform integration are incorporated in the on-board missile computer. Accelerations are measured by accelerometers, the principle of which is best illustrated by a pendulum. Fig. 614-a shows a pendulum supported by a pivot through a crosspiece. If the crosspiece is accelerated to the right, as shown in Fig. 614-b, the pendulum will swing to the left by inertial reaction.
This same effect of inertia is experienced in a car when the driver steps on the gas. As the speed of the car increases you are pressed back against the seat.
Decreasing speed produces an opposite effect. When the brakes are applied you tend to fall forward. In an accelerometer, the direction of reaction indicates acceleration or deceleration (Fig. 614-c), and the amount of reaction gives the value. The accelerometers are allowed to swing in only one plane, thus measuring changes of velocity in only one plane-two directions, one opposite the other. During flight the course is controlled to keep the lateral deviation from the correct path equal to zero. This keeps the missile on course. Fig. 615 shows two of the many trajectories that may be used by the surface-to-air missile.
Fig. 615. Surface-to-air trajectories.
Path 1 is an up-and-over type trajectory. On this path the missile quickly climbs out of the more dense lower atmosphere, and flies the greater portion of its course to the target in the less dense, higher atmosphere while the straight line type trajectory is just the reverse.
A missile following this path to the target spends the major part of its flight in the dense, lower atmosphere, and during the terminal phase must climb steeply to intercept the target. Path 1 is a more efficient trajectory. The straight line trajectory is almost impossible to achieve except at close range.
Command guidance
A command guidance system is much like that used to control planes. In this system the missile, too, is steered by commands sent to it by radio from a control station.
The control station keeps track of the relative positions of the target and the missile by using two radar-like systems, one of which tracks the missile while the other tracks the target. A computer takes this information and generates the command signals to be sent to the missile. In a typical command system, as shown in Fig. 616, the missile tracker and the target tracker feed missile and target position data to the computer, which in turn generates commands that are transmitted to the missile over the missile-tracking radar beam. The missile can thus be directed to fly on almost any trajectory to the intercept point.
Beam rider control
In a beam rider guidance system ( Fig. 617) the missile steers itself along the axis of a guidance beam.
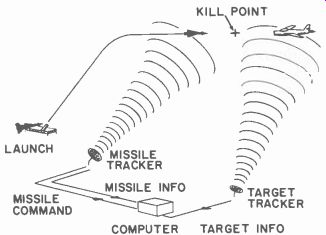
Fig. 616. Command guidance operation.
While any beam of energy, such as visible light or infrared, might be used, the more practical system uses a radar beam. In the simple case of the single-beam rider, the radar beam tracks a target in the air. The missile is launched into the beam where a receiver and computer in the missile maintain the position in the beam as it climbs to intercept the target.
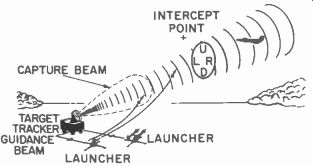
Fig. 617. Single-beam rider. Missile steers itself in radar beam.
Homing guidance
Homing guidance is a system wherein a missile finds a target and steers itself toward it.
A homing guidance system consists of a target seeker in the missile, receptive to energy which is being radiated or reflected from the target, and a computer which gets data from the target seeker and sends appropriate commands to the missile control surfaces, which keep the missile headed toward the target.
Characteristics of the target which may be used by the seeker for homing include: radar reflectivity; light, radio and sound emissions; infrared (heat) emissions; and magnetic and capacitive features. Homing guidance may be classified as active, semi-active or passive.
An active homing system (Fig. 618-a) is one in which all of the guidance equipment is contained aboard the missile. This includes a transmitter that illuminates the target, a seeker to receive reflected energy from the target and a computer. Once the active homing missile is launched, it acts independently of any outside agency and follows a correct path to the target.
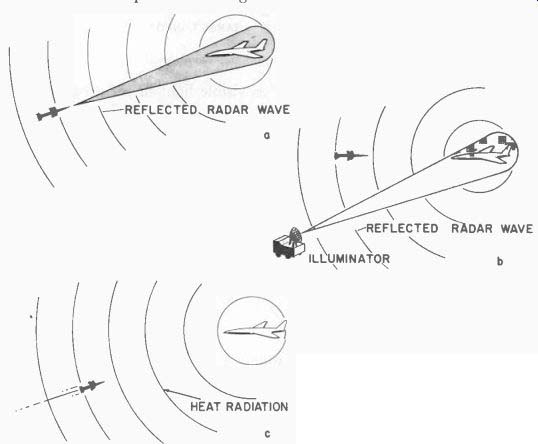
Fig. 618. Active homer [a]. Missile illuminates target. Semi-active homer
[b]. Ground radar illuminates target. Passive homer [c]. Missile senses heat
radiations from target.
In the semi-active homing system (Fig. 618-b) only the target-seeker receiver and a computer are contained aboard the missile. The target is illuminated by some outside source, usually an airborne or ground radar. After the missile is launched the target must be continuously illuminated until intercept.
A passive homing system ( Fig. 618-c) makes use of the natural emanations from the target, such as infrared rays from engine heat or radio emissions. Since the target illuminates itself, the passive homing system acts independently of any outside agency in following its course to intercept.
Telemetry---Telemetry means sending information from afar. In the telemetry system, however, we place the transmitter in the remote or moving location. Instead of sending commands back, it sends signals to the receiver from measuring instruments, which we can use immediately or record for future analysis.
One of the simplest telemetry systems is probably the Doppler system (so named because of the principle involved) which will give information on speed and position in space.
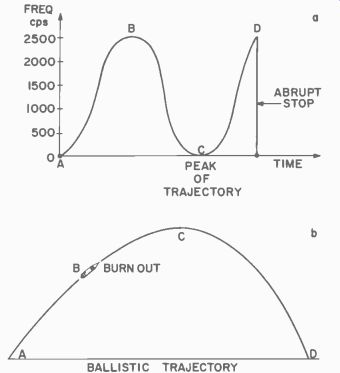
Fig. 619. The radial velocity of the rocket can be calculated by dividing
the beat frequency by the frequency of the transmitter
[a]. Ballistic trajectory is shown in drawing b.
A small crystal-controlled transmitter will send out a pure carrier.
We can pick this up on a receiver and at the same time we can feed in a signal from a signal generator, which is tuned to exactly the same frequency as that of the transmitter until the two signals are exactly at zero beat.
When we put this transmitter in a rocket and launch it, there is an effect (the Doppler effect) which is the same as that noticed while listening to the horn of an approaching car or train. As it speeds toward you, the pitch of the moving sound generator is higher than when it is not moving. As the sound generator passes the pitch lowers.
The same is true of the transmitter in the rocket or missile. As the rocket speeds away, increasing its distance from the launching site, the frequency of the signal sent out by its transmitter will arrive at the receiver lowered by an amount proportional to the speed of the rocket. This will produce a beat note which will be plainly audible to the human ear if the signal generator is kept tuned exactly to the frequency of the transmitter before the rocket was launched.
As the rocket is launched the speed of the moving transmitter will cause a frequency difference at the receiver which will be indicated by an increasing tone pitch. The sound we hear starts at a very low note, increases to some higher tone as the acceleration continues, decreases to zero again, and then begins increasing up to some high pitch where it will abruptly stop when it crashes into the ground. A graph of this effect is shown in Fig. 619, where the changing pitch is shown in relation to the trajectory. As the rocket speed increases and reaches a maximum, the pitch increases. The motor burns out at B, which is the highest pitch. The rocket then coasts on up to its peak altitude, decreasing in speed as it does so. As its speed decreases, the pitch also decreases. At the peak, the rocket is neither moving away nor returning to us, so the pitch is zero. When the rocket, under the pull of gravity, begins its descent, its speed again increases, and again we hear the tone increasing in pitch. The maximum velocity of the rocket is reached just as it hits the earth. Therefore, we hear at that moment the highest pitch and then silence. By listening to the tone of the receiver output, we can tell when the rocket has reached its peak, and if we clock the time it takes to reach the peak we can determine roughly its altitude, since the distance it will fall is:
S= Y2gt2
( Where g is the gravitational constant, 32.2 feet per second, and t is the time the rocket is falling.) A very close approximation is that it will fall for as long as it took to reach peak altitude. Note that this situation will be true only for the high angle overhead shot. In ballistic trajectories the pitch will not decrease completely to zero at peak altitude since the rocket is still moving away from the ground receiver.
It is possible to determine the rocket speed from this tone information, knowing the frequency of the radio carrier. The tone we receive, in cycles per second, is exactly equal to the number of wavelengths per second that the rocket is moving away from the receiver on a radial path. Let us use, for example, 144 mhz, which has a wavelength of about 6.86 ft. At ten seconds after launching, if the tone is 1,000 cycles per second, the rocket speed is 6,860 ft. per second. The highest pitch tone at that instant (averaged over a one-second interval) would give the maximum rocket speed.
The next step would be to try to collect other data like temperatures and pressures. This can be done if we modulate the transmitter with a number of tones and make each tone vary with the quantity we want to measure. Note that this means we must have small audio oscillators capable of having frequencies controlled with potentiometers, by variable capacitors, inductors, or by means of a voltage.
The procedure would be: First, calibrate the audio oscillator and set up a chart as shown in Table 6-1 (we assume that what we are to measure can be converted into an angular change).
Table 6-1

Audio oscillator and potentiometer calibration
Potentiometer wiper position
Tone (hz) Centered 600 10 degrees right 650 20 degrees right 700 30 degrees right 750 10 degrees left 550 20 degrees left 500 30 degrees left 450
We must be certain that the temperature and vibrations of the rocket will not cause changes in these calibrated figures.
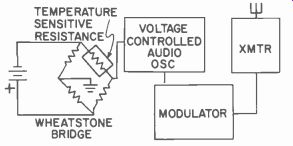
Fig. 620. Measuring nose skin temperature and telemetering this in formation
to earth.
Next, place the transmitter, modulator and oscillator in the rocket.
Connect the potentiometer to, say, a fin shaft in such a way that, when the fin is neutral, the arm of the potentiometer is centered. We launch the rocket, receive the modulated signal on our receiver, and pass this signal through a discriminator tuned to a rest frequency of 600 hz.
The output of the discriminator is recorded on a moving chart.
If the fin is turned, we can tell from the lines made automatically on the chart how much, how fast and when it turned. Thus, we can measure physical variations of the rocket while it is in flight. We could use different tones to transmit many channels of information.
Fig. 620 shows how a voltage-controlled oscillator can be used to measure the rocket nose temperature. In this case, the oscillator would be calibrated in terms of the bridge unbalance per degree of temperature.
As in radio control, there should be frequency separation between the bands of frequencies used for telemetry purposes. For example, we used the band 450 to 750 hz for the fin measurement. Now we want to jump up the scale a little, say to 1,000 to 1,500 hz, for a band measuring nose temperature. The separation of the bands makes the...
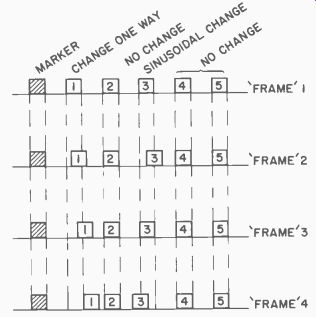
Fig. 621. Pen-recorded tape cut into frames for analysis.
... decoding problem easier and more accurate. In the case of multiple tones or bands, we would have to feed the receiver output through bandpass filters before sending it to various discriminators.
This method of telemetry is called continuous because all information is sent back all the time. From the discussion of radio control systems using tones, remember that it is not wise to send more than 6 or 8 tones simultaneously because of the modulation percentage allotted to each. That holds true also for this system.
When we want to get more information, say from 30 to 120 channels at a time, we use pulses and pulse trains to do the job. The modulation percentage is 100 percent for each pulse, and the speed of transmission is so high that it is almost like getting continuous information. Whatever we measure should be sampled at least seven times per second. This is the minimum number of samples needed for accurate reconstruction of a sine wave-like variation. In case the measured quantity is not expected to be a sine-wave function, it will be necessary to take more samples per second in order to recon struct an accurate curve.
The method of using pulses is also very similar to that in radio control. Pulse width, amplitude, or spacing variations can be used to convey the intelligence. Fig. 621 shows how a tape might look which contains four frames (a frame is a complete pulse train), and how each pulse might be varied in time. The vertical lines then, through the same numbered pulses, show the variation in the measured quantity.
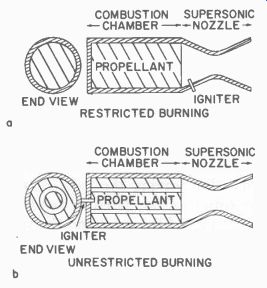
Fig. 622. Solid-propellant rockets.
Propulsion
The rocket engine furnishes the power which drives the rocket or missile into space. There are many types of jet propulsion devices.
Let us examine some basic principles of rockets, both the solid and liquid propellant types.
There are two general types of solid fuel rockets, the restricted burning and the unrestricted burning types. In the restricted burning method, the propellant one end only (Fig. 622-a) and the fuel burns like a cigarette. This type gives thrust for a longer time than the unrestricted burning method.
In the unrestricted burning type rocket, the fuel, which is cast in solid form, is molded or slotted (Fig. 622-b) so that it burns throughout its length. This type of rocket produces a much higher thrust (or push) for a much shorter period of time.
Every rocket engine has a nozzle. This is the tapered and flared exhaust section shown in Fig. 623. The nozzle has converging and diverging sections; these tapers are very important in getting the most power from the rocket. The converging section causes the gas velocity to increase until sonic speed (the speed of sound) is reached at the throat. The diverging section further increases the velocity by allowing the gases to expand rapidly out into the atmosphere. The expanding gas at the exit can reach a velocity higher than 2,000 feet per second.
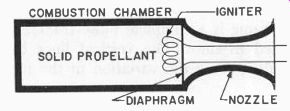
Fig. 623. Typical rocket motor or engine.
There is a popular belief that the rocket produces thrust when the exhaust gases push against the air. This is not true, because the rocket can operate in a vacuum and in space. What actually happens is that the mass of gases pushed out of the rocket combustion chamber at high speeds causes a reaction on the rocket. This reaction is what produces the thrust.
A simple example of the force produced by such a reaction is the kick of a shotgun against one's shoulder when the lead pellets fly out the barrel (Fig. 624). Another way to show the effect of reaction is to put on a pair of roller skates and throw some heavy rocks or bricks forward. Your effort in throwing the bricks forward will produce a reaction that will move you backward. The important point in the rocket is that, even though the gas molecules are very small and have very little mass, they move at such tremendous velocities that large reactions are produced.
The thrust (F), then, is obtained by increasing the velocity (V) of the gases from a zero value inside the combustion chamber to a very high value leaving the exhaust nozzle. This is called increasing the momentum of the gases. Momentum is the quantity of motion and is the product of the mass and the velocity (V) of the gases. The mass of an object is its weight divided by the gravitational constant 32.2.
The rocket-thrust equation can be written:
F = (Momentum at exit)--(Momentum in chamber) time to move from chamber to exit Or F = (Mass X exit velocity)--(mass X chamber velocity) time or mathematically:
X V.
F= W X V.
t g X t
Where W is the weight in pounds, g is 32.2, t is time in seconds and Ve is the gas exhaust velocity in feet per second. The part of the equation Wt is the amount of propellant burned per second.

Fig. 624. Action equals reaction.
Now an example to clarify the thrust equation: Assume that we have a propellant weighing 10 pounds and that this particular propellant, when burned in a combustion chamber which has a proper nozzle, produces an exhaust-gas velocity of 1,000 feet per second.
Assume also that this burns 5 pounds of fuel per second. What is the thrust produced?
X 5 (pounds) 1 1,000 ( ft/sec.) - 1 (second) 32.2 1 5,000 = 155.28 pounds of thrust for 2 seconds 32.2
Since we have 10 pounds of fuel and burn only 5 pounds per second, the engine will burn for 2 seconds. If we increase the burning rate (pounds per second) the thrust will increase, but last for a shorter time. Conversely, if we decrease the burning rate the thrust will decrease, but last for a longer time.
Chemical reactions
Since the energy which propels the rocket comes from chemicals, let us analyze chemical reactions, particularly the reaction of zinc and sulfur, which we will use as the propellant in the rocket we design in the next section.
The energy which propels the rocket comes from a chemical reaction, or from the burning of chemicals. This process releases energy in the form of heat. The heat in turn produces kinetic energy, which is the energy of motion.
One simple chemical reaction which produces heat is the combustion of hydrogen (H2) and oxygen (O2) to form water plus heat.
There is a way to show this reaction by means of symbols in an equation:
2H2 + 02--> 2H20 + heat
The arrow indicates that the hydrogen molecule plus the oxygen molecule change to water (2H20) plus heat.
Perhaps you recall mixing an electrolyte, using distilled water and sulfuric acid. When the acid was poured into the water the mixture also developed heat. This is another chemical reaction which produces heat.
Another heat-producing process, not normally thought of as combustion, is the reaction between zinc (Zn) and sulfur (S) to form zinc sulfide (LS). This can be stated as a chemical equation:
Zn S--> LS + heat
This is the basis of the propellant we will use in our model rocket design problems.
Proportion of powders
We will use two powders, zinc and sulfur. To know how much of one to mix with the other, we must apply the law of balanced chemical equations.
We must determine the formula weights of the chemicals to be used.
The formula weight is equal to the sum of the weights of the atoms indicated by the formula. The atomic weight of zinc is 65.38 and that of sulfur 32.07.
Now we also know something else from the chemical law. In the case of the combination of hydrogen and oxygen to form water plus heat, 2 atoms of hydrogen combine with 1 atom of oxygen, as denoted by the 2 in front of the hydrogen symbol. In the present case, 1 atom of zinc will combine with 1 atom of sulfur to produce the zinc sulfide and heat. We know this because there are no numbers in front of the parts of the equation. The formula weight then is:
The number of atoms of zinc times the atomic weight of zinc, plus the number of atoms of sulfur times the atomic weight of sulfur. The formula weight can now be stated symbolically as:
Formula weight = (1 X 65.38) (1 X 32.07) = 97.45
This means that we want the same ratio for any amount of propellant as the ratio we would get by mixing 65.38 pounds of zinc with 32.07 pounds of sulfur for a total of 97.45 pounds of zinc sulfide propellant.
We will not usually want a quantity as large as 97.45 pounds. We want to know the proportions of zinc and sulfur needed to mix, say, 1 pound of propellant. The formula is:
65.38 + 07= 1 pound of propellant 97.45 97.45 or for a more practical amount:
0.67 pounds zinc plus 0.33 pounds sulfur = 1 pound propellant
If we want more propellant, we can now multiply these two numbers (0.67 and 0.33) by the number of pounds of propellant we want. If we want 10 pounds of propellant we would have to mix 6.7 pounds zinc with 3.3 pounds of sulfur.
Another useful thing to know is the ratio by weight of one chemical in the formula to the other. We find this by dividing the larger number by the smaller:
Ratio = 65.38= 2.04 32.07
This means we always use 2.04 parts by weight of zinc to each part of sulfur.
Liquid propellant rockets
To overcome weight and cooling problems for long-duration units, liquid propellants are used. In most liquid propellant rockets, one of the propellants enters the rear of the engine, flowing between the walls, cooling the inner surface, and making thin-walled combustion chambers possible.
In the process of flowing through and cooling these surfaces, the propellant itself is heated; it then enters the forward end of the combustion chamber.
This is known as regenerative cooling. Heating the propellant results in more efficient combustion and because the engine is cooled, long-duration burning is possible. The operating pressure in the combustion chamber is only 250 to 500 pounds per square inch (psi), and since the propellants are stored outside the combustion chamber, the construction may be lighter in weight than comparable solid propellant rockets ( considering those beyond a certain impulse or power ).
Propellant systems
Two methods are used for supplying the rockets with fuel and an oxidizer from tanks. These are the pressure feed system and the pump feed system (Fig. 625).
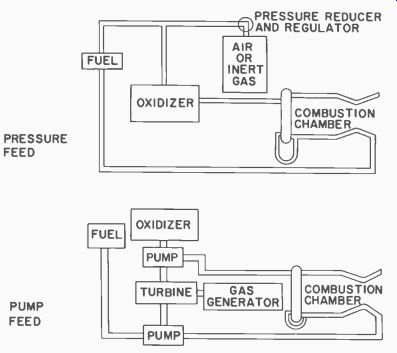
Fig. 625. Liquid-propellant rockets.
The pressure feed system is the less complicated of the two. Pres sure is supplied to both the fuel and oxidizer tanks. The pressurized air (or an inert gas such as helium) is fed through a reduction valve to the two tanks at a pressure of about 500 psi, when the chamber pressure is approximately 300 psi. (As a rule of thumb, the pressure on the propellant tanks must be about 200 psi greater than the operating pressure in the combustion chamber.) To supply pressure for the duration of burning, which may be as long as 50 to 60 seconds, the pressure tank is originally charged to at least 150 atmospheres (about 2,200 psi). With a pressure of 500 psi or greater on the propellant tanks and 2,200 psi in the air bottle, these tanks must be of heavy construction. As the size of the rocket increases, the impulse weight ratio decreases, until finally the empty weight of a pressure-feed rocket becomes a serious disadvantage compared to the empty weight of a pump-feed liquid rocket with the same impulse. This condition is reached at about 5 tons. However, the pressure-feed system is the more economical of the two for light-weight rockets.
In the pump-feed system, hydrogen peroxide may be combined with sodium permanganate as a catalyst in a gas-generating system.
Combining in the reaction chamber, they generate steam, which is used to drive the turbine, which in turn drives the two pumps.
Pressure is felt only on the downstream lines. Consequently, the fuel and oxidizer tanks can be of much lighter construction. The pump-feed system is far more complicated than the pressure-feed system, but there is a great weight saving, since there are no large air bottles and since thick-walled fuel and oxidizer tanks are not necessary.
Another method is to place a small turbine in the exhaust jet, which drives the pumps, which in turn give the necessary pressure on the...

Fig. 626. Hercules and Ajax rockets use liquid propellants.
...fuel and oxidizer lines. The Army Hercules and Ajax rockets are examples using liquid propellants ( Fig. 626 ).
Atmospheric jets
Two of the undesirable characteristics of rockets are short burning time and high rate of propellant consumption. To remedy these disadvantages, the pulse-jet, ram-jet, and turbo-jet utilize atmospheric oxygen ( air) and carry fuel only.
Pulse-jet
Fig. 627 shows the cross section of a typical pulse-jet. It consists of a tubular section, with a set of spring-loaded valves and a means for injecting fuel, followed by a combustion chamber and a tailpipe.
At the start of the operating cycle, the fuel is sprayed into the combustion chamber and is then ignited by a spark plug. The gases formed by combustion create a pressure of 25 to 35 psi. The spring-loaded valves prevent the gases from escaping through the intake so they rush out the tailpipe at high velocity, thus over-expanding and causing a partial vacuum inside the combustion chamber. This makes the valves open and draw fresh air into the combustion chamber.
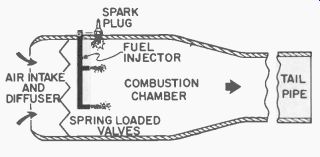
Fig. 627. Pulse-jet.
Part of the exhaust gases flow back up the tailpipe and meet the air coming in through the valves, which slightly compresses the new air.
This compression, plus residual burning vapors, ignites a new charge of fuel, which is being sprayed continuously into the combustion chamber. Thus the action is intermittent, giving rise to the name intermittent jet, pulse-jet.
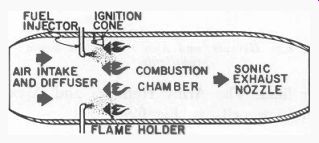
Fig. 628. Subsonic ram-jet.
Subsonic ram-jet
Assume that the ram-jet in Fig. 628 is operating at a speed less than the speed of sound. Air will flow through the ram-jet, which consists of a tubular section, with a diverging forward section or diffuser. As air flows through the tubular section, it loses velocity, since the cross sectional area increases.
The energy in the air stream is in the form of pressure energy and velocity energy. If the velocity decreases, the pressure must increase to keep the total energy constant. This is exactly what happens in the ram-jet; this increases the pressure, and makes the pressure at the forward end of the combustion chamber greater than the pressure in the free stream. Fuel is continuously injected into the air in the dif fuser. The ignition cone, which is similar to the pilot light on a gas stove, maintains an ignition flame. The air-fuel mixture passes through the flame holder, which is a grid-work of V-shaped metal troughs. Part of the mixture swirls into the troughs and is ignited there by the ignition cone. The major portion of air and fuel passes on through the flame holder, which sets up a turbulence helpful for good mixing.
It is ignited by the burning mixture in the flame-holder troughs.
Combustion continues while the flow moves back through the combustion chamber.
The combustion gases want to expand in all directions, but are restricted by the combustion-chamber walls and the high-pressure area at the rear of the diffuser. Consequently, the gases are accelerated out the tailpipe. This is reaction and the thrust, which is also applied internally to the diffuser section.
Supersonic ram-jet
The supersonic ram-jet (Fig. 629) works essentially in the same way as the subsonic ram-jet. The major differences are in the diffuser and exhaust sections.
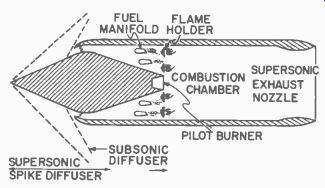
Fig. 629. Supersonic ram-jet.
The diffuser is a protruding conical spike. The spike aids in the pressure recovery (the process by which velocity energy is exchanged for pressure energy) (Fig. 630-a).
When the ram-jet has been boosted to a supersonic speed, it is necessary to reduce the flow of air into the chamber to a subsonic velocity. A shock wave must be formed. If the subsonic type of diffuser is used, a normal shock wave will be formed; that is, one perpendicular to the flow of air.
A normal shock wave has two important characteristics; a large percentage of the flow of energy in a strong shock wave is dissipated as heat and the flow behind the shock wave is always subsonic. To realize a more efficient conversion of the flow energy the supersonic or spike diffuser was developed. By first changing the direction of flow, a conical shock wave is created which lowers the velocity (though not necessarily to a subsonic value), and is much more efficient in the conversion of flow energy to pressure than the normal shock wave. After passing through one or more conical shock waves, the air passes through a weak normal shock wave and enters the sub sonic diffusion area. Thus a relatively high compression is realized and energy losses are minimized (Fig. 630-b).
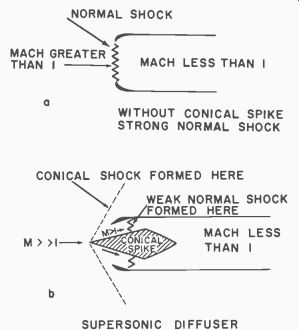
Fig. 630. Shock waves for supersonic diffuser.
After compression the fuel is added and the burning takes place downstream from the flame holder in the combustion chamber, exactly as in the subsonic ram-jet.
Turbo-jet
The most common jet engine is the turbo-jet. It is possible to use this jet engine in aircraft because it is capable of developing sufficient static thrust to let the aircraft take off under its own power.
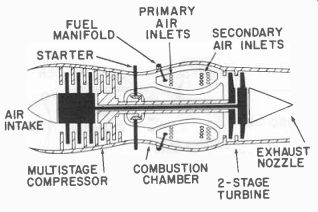
Fig. 631. Axial flow turbo-jet.
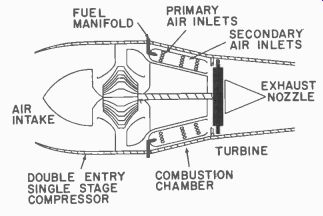
Fig. 632. Centrifugal flow turbo-jet.
The turbo-jet operates on the same principle as any other atmospheric jet engine. A quantity of air must be taken in and compressed and fuel added. The mixture burned in a combustion chamber expands and these products of combustion are accelerated rearward with increased momentum.
The turbo-jet consists of a compressor (which may be either axial (Fig. 631) or centrifugal ( Fig. 632) ), a combustion chamber, a method of introducing fuel, an exhaust for accelerating the combustion products and a turbine just ahead of the exhaust to extract power for driving the compressor. To start operation, the compressor must first be brought up to nearly 20 percent of normal operating speed to raise the pressure in the combustion chamber so that combustion can be accomplished. Fuel is then injected into the combustion chamber and ignited. Since combustion produces a temperature high enough to ruin the turbine blades, secondary air is introduced, which lowers the temperature of the jet stream to about 1500°F before this stream reaches the turbine blades which are on the same shaft as those of the compressor. Hence, the hot-high-velocity gases passing through the turbine cause it to rotate, imparting rotation to the compressor.
Turbo-jet with afterburner
The afterburner is a thrust-increasing device that mixes the unused air (oxygen) in the turbo-jet exhaust with other fuel, producing more thrust. The afterburner is nothing more than a subsonic ram-jet attached to the turbo-jet (Fig. 633).
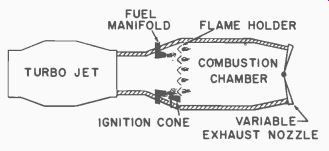
Fig. 633. Turbo-jet with afterburner.
... air. To utilize this air an afterburner consisting of diffuser section, fuel injection device, flame holder, combustion chamber, and exhaust nozzle is attached to the exit of the turbo-jet. After diffusion, more fuel is injected and the mixture is burned again. This results in a temperature much higher than the 1500°F which was the maximum allowable in the turbo-jet. Energy is added in the form of fuel, converted to thermal energy, and finally converted to kinetic energy by reaction. This added thrust increases the momentum of the mass as it passes out of the afterburner exhaust nozzle. While the afterburner is operating, the variable exhaust nozzle is opened to prevent the temperature and pressure from backing up into the turbo-jet. An increase in thrust of about 40% is realized with afterburner operation. Fuel consumption increases approximately 250%. Because of the increased use of fuel, the afterburner is used only when extra thrust is needed.