AMAZON multi-meters discounts AMAZON oscilloscope discounts
Now we will show the calculations which must be performed to design a model rocket. Methods of construction, ways of launching and firing will also be discussed. The calculations are not difficult and an effort has been made to make them as clear as possible.
A model rocket is not a toy. It is a most dangerous instrument when treated lightly. We shall first devote a few words to that all-important topic of safety.
Safety precautions
Most states and many municipalities have enacted legislation banning the sale, manufacture and firing of fireworks by unlicensed persons. Rockets and rocket fuel are similar to fireworks in many respects, so it is important that anyone who plans to venture into amateur rocketry learn about local laws so that all activities can be conducted on a legal basis.
When rockets are transported on state highways they must be handled in accordance with the laws of that state and the laws governing interstate commerce. It is best to consult your state highway patrol or similar organizations for this information.
When rockets loaded with propellant are transported on a military reservation, the igniter must be packaged separately. The transporting vehicle must be clearly marked explosives on the front and rear sides.
Each vehicle must be equipped with two fire extinguishers.
Because a rocket can present a hazard to air navigation one should also think of the possibility of legal problems which may be encountered. In general, the rocket must be fired into an airspace from which aircraft are restricted, or clearance must be obtained from the Civil Aeronautics Authority. In any event, remember that even the airspace is regulated and cannot be used indiscriminately.
Before entering into any type of amateur rocket activity either in a group or as an individual, it is advisable to secure expert legal guidance concerning your liability responsibilities as to property damage, injury or death to live stock. Injury, even to an uninvited spectator trespassing on your own private firing range, could result in costly and unpleasant court action.
Do not experiment with model rockets without proper supervision and guidance. Students can often enlist the aid of a teacher who, in turn, can contact military agencies and obtain guidance and assistance from persons and agencies who are experts and engaged professionally in the handling of rockets. Do not take chances. Plan. Take extra precautions. Get help from experts. Enjoy this hobby and live! Handling of propellants The zinc and sulfur micrograin propellant is the best type for amateur rockets on the basis of both performance and safety. The following rules should be rigidly adhered to in its handling:
1. Handle and mix only under direct, expert supervision.
2. All equipment used in mixing must be connected to an electrical ground to guard against accidental sparks from static electricity. An electrical ground connection may be made to a water line or a metal rod driven into the earth. All metal parts must be connected ( bonded) together by flexible wires which are connected to the ground. The ends of the wires should be bright and clean and all connections tight and incapable of being loosened by accident.
3. Allow no open flames or sparks in the mixing area.
4. Do not heat or cook mixtures.
5. Do not grind or apply heavy pressure or subject mixture to shock.
6. Do all mixing out of doors.
7. Do not allow excessive micro-grain dust to accumulate in the air.
8. Allow only the minimum number of essential people near the mixing and loading operations or near the loaded rocket.
9. Handle as small a quantity of propellant as possible.
10. Mix the propellant near the launching site.
11. Do not load rocket until ready to fire.
12. Wear flame-resistant and protective clothing.
13. Have fire-fighting, rescue and first-aid equipment standing by during all propellant-handling operations.

Fig. 701 . Guided missile being loaded with liquid fuel.
Fig. 701 shows the loading of a guided missile with liquid fuel. Note the protective clothing worn. Fuel is carefully measured before being pumped into the rocket-fuel tank.
Dangers of other propellant types
Most other types of propellants are considered too dangerous to be handled by amateurs or hobbyists. This applies especially to the readily available chlorates like sodium chlorate and potassium chlorate. These explode very easily when rubbed, ground or mixed-they are not even used in military or scientific rockets! The dust of powdered metals such as iron, magnesium, nickel and aluminum can form explosive mixtures with air when poured from one container to another, or when shaken. The dust of some of these metals can ignite spontaneously while floating in the air. When these metals are mixed with an oxidizer they become sensitive to shock.
(An oxidizer furnishes oxygen to the mixture.) Most people know that nitroglycerine will explode violently on slight shock, and is sensitive to heat. Nitrocellulose can also explode when subjected to heat or shock and it burns easily in the open air when ignited. Metallic sodium, metallic potassium and yellow phosphorus all ignite spontaneously when exposed to air. Liquid propellants generally present additional hazards such as poisonous fumes, extreme corrosion and spontaneous ignition.
Rocket firing operations
Firing of rockets should be confined to approved firing ranges and conducted under the supervision of qualified individuals. Firing procedures should be carefully and painstakingly thought out, and written out, step by step, in advance of the firing. The procedure should be checked by experts, practiced with an unloaded rocket until letter perfect and then carefully followed in the actual firing.
The rocket ignition system should not be connected until just before firing and should always be of a type that can be activated electrically from the safety of a distant bunker. The connecting of the firing mechanism should be one of the very last steps performed, and should be done only when all personnel are in a place of safety.
All persons connected with the firing should be in safety bunkers with overhead protection when the rocket is fired. A rocket should never be launched exactly vertically nor should it be launched during a strong wind. The rocket when fired exactly vertically endangers the launching site--it may not go as high as expected--it may explode just overhead and fall back on the launching crew. Strong winds can cause the rocket to go off course and endanger persons or property.
In the event of a misfire (the rocket doesn't go off when the firing switch is closed) try to fire it a minimum of three more times. If it still doesn't fire, wait at least thirty minutes before approaching the rocket. Disconnect all wires to the firing device before approaching.
After a successful firing everyone should remain under cover until it is certain that the rocket has returned to earth.
Safety summary
The rocket hobby, while enjoyable, can also be a life-and-death matter. Use only a recommended propellant. Design the rocket with the greatest care so that it has the best chances to perform as expected.
Static test (ground fire) the rocket before launching. Observe all the safety precautions mentioned earlier. After the rocket has been static tested, load the propellant and connect the igniter only at the site of the actual launching after being certain that the static firing has caused no weakening of the structures. Expose a minimum number of people to the loaded and armed rocket. By using extreme caution and care you can have a successful and safe firing. You can make your rocket hobby a gratifying, worthwhile experience instead of a tragedy.
Costs and equipment
A single rocket about two inches in diameter and four feet long will cost about $35.00. The propellant, mixing and ignition system will cost about $40.00 additional. Much of the launching equipment can be made and then used over and over again. Sometimes the rockets themselves can be recovered by means of parachutes and, if they remain sound, can be used again.
Stop watches, movie equipment and some electronic equipment will be needed to give purpose and meaning to this hobby. These are best obtained through a club effort. If a club is formed, costs can be shared. Often guest speakers can be obtained for meetings and time can be spent studying designs between the actual launching activities.
Learn as much as you can about the theory of the devices involved.
Set specific objectives for each launching to increase the knowledge of the club members. A lifetime career in space technology may well start from this beginning.
Design of a model rocket We will now show how to design a model rocket to meet the following specifications:
a. To have a thrust of 800 pounds for 0.5 second.
b. To use zinc and sulfur as the propellant.
The procedure is as follows:
a. Determine the amount of propellant needed.
b. Determine the diameter of the burning surface.
c. Determine the length of the propellant.
d. Determine the thickness of the combustion chamber walls.
e. Determine the dimensions of the exhaust nozzle.
There are certain other bits of information which are needed for the design, especially those concerning the propellant. These can be calculated but the mathematics are beyond the scope of this text.
Instead we will just state these as facts and use them in our design.
Remember, the factors in Table 7-1 apply to the zinc-sulfur propellant only.
Table 7-1 Characteristics of Zinc Sulfur Propellant
a. Effective exhaust velocity (VP) = 1490 lbs/ft/sec.
b. Chamber pressure ( Pa ) = 1,000 lbs/sq. in.
c. Chamber temperature ( Ta ) = 3060° Rankine
d. Molecular weight ( Me) = 97.45 lbs/mole
e. Specific heat ratio (y) = 1.25
f. Density (D) = 161 lbs/cu. ft.
=- 0.0932 lbs/cu. in.
g. Burning rate (r)
h. Gas constant (Particular)
i. Thrust coefficient ( Cf)
= 90 in./sec.
= 15.8 ft/degree
Rankine = 1.57 As a point of information, some temperature conversion factors are:
Rankine = F 460° Kelvin = C 273° Centigrade = 5/9 (F--32° )
Solution:
The weight of the propellant ( We) required can be found by using the thrust equation:
F = gt X V, or F = m X Ve where m is the mass of propellant burned per second.
For our problem we rewrite the equation:
F = I' X V, to X g where We is defined above, to is the burning time and g is the gravitational constant 32.2 ft/sec'. Then:
WP= F X tb X g Ve and inserting the values for these letters, 800 X 0.5 X 32.2 We = = 8.64 lbs. of propellant required 1490 Remember that we are using a ratio of 2.04 parts of zinc and 1 part of sulfur (3.04 part total) so the proper weights of each will be :
04 Weight of zinc = 2.X 8.64 = 5.80 lbs of zinc powder.
3.04 Weight of sulfur can be either 8.64--5.80, or 2.84 lbs, or can be calculated by using the ratio:
1 Weight of sulfur =-3.04 X 8.64 = lbs of sulfur powder.
Weight of propellant burned per second To determine the proper shape of the propellant we must determine the burning rate. We want all propellant burned in 0.5 second and we know how many pounds of propellant are necessary, so the burning rate is simply :
total propellant weight burning time 8.64 lbs of propellant, 17.28 lbs per second 0.5 second
The burning surface This can be determined easily since the volume of propellant burned per second equals the burning surface area (S) times the burning rate (r). The volume burned per second also equals the weight per second burned divided by the density (D). From the above we can write two equations and using these, can find the burning surface and from that the diameter of propellant required.
(1) V=SXr (2) V = W tbp X 1/
We equate (1) to (2) :
SXr=W--2 X th D
Inserting the numerical values known, or found previously, and solving this equation for (S) :
Wp t S--b r X D 17.28 lbs sec.
S 90 (in. per sec.) X 0.0932 lbs/in3 17.28 S = = 2.06 square inches 90 X 0.0932
So our propellant must have an end area of 2.06 inches.
Generally, the rocket chamber is in the form of a cylinder or pipe, so this square-inch end area becomes an equivalent circular area from which we can state the tube diameter. Since the area of a circle is (r) (diameter)2 all equal to re or we have to do is to set this equation equal to 2.06 and solve for the diameter.
S ( 7 ) ( diameter )2 4 ,then 4 S
= (Ti-r)diameter, and (4) (2.06)
= 1.625 inches 3.14
So our rocket combustion chamber must have an inside diameter of 1.625 inches.
The length required is equal to the burning rate times the total burning time:
90 inches per second X 0.5 second = 45 inches At this stage, then, we know in what proportion the propellant must be (zinc and sulfur), and the size of the combustion chamber (tube or pipe) that it will be put in. Next the thickness of the pipe walls must be determined. We don't want our rocket to blow up when we try to launch it.
The tensile strength of the materials to be used is our next concern.
If we use a low-carbon steel for the propellant tube that has a tensile strength of 62,400 psi (SAE 1020) we divide that rating by four and assume that it can stand only 15,600 psi.
62,400 = 15,600 4
This gives a safety factor of four. This safety factor is necessary because the extremely high temperatures that are generated by the burning propellant reduce the strength of the steel considerably.
The wall thickness is determined from the equation:
chamber pressure X radius allowable stress The pressure inside the chamber was given as 1,000 pounds per square inch. The inside radius of the pipe is 0.81 inch, and the stress is the factor we computed above, 15,600 pounds per square inch. The wall thickness then is:
1,000 X 0.81 - 0.0519 inch 15,600
A steel tube with a wall thickness of 0.0625 inch, about equal to 16 gage, will do nicely. The tube must have an outside diameter of 1.75 inches and an inside diameter of 1.625 inches will fulfill the requirement.
The final part of the rocket to be calculated is the nozzle. We must calculate the throat- and exit-area diameters (Fig. 702). These dimensions are very important since they determine the maximum efficiency from the exhaust gases and thus maximum thrust.
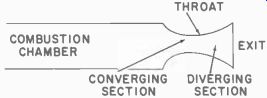
Fig. 702. DeLaval nozzle adapted for rocket engine.
Additional information is needed to make these calculations. This is given in Table 7-2.
Table 7-2 Coefficient of Thrust (Cr)
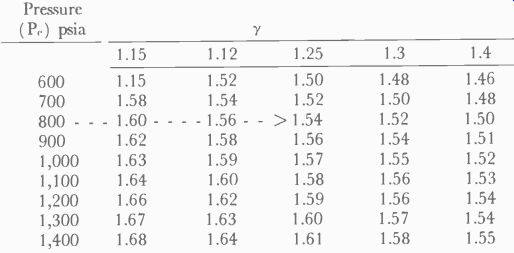
To find the value of Cr needed, we enter the table horizontally opposite 800 pounds (the thrust value initially assumed) to the column headed by 1.25, the value of gamma (y) given in Table 7-2. At the intersection we obtain the value 1.54 to use in the formula:
Force = Cr X At X Pe First we must solve this formula for At and we get:
At (area of throat) = F Cf X Pe
Our force (thrust) is 800 pounds, the Cr just determined is 1.54, and P, was given earlier (Table 7-1) as 1,000 lbs/sq. in. Inserting these values in the equation and solving for the throat area:
800
At =
1.54 X 1,000 gives us 0.51 square inches as the answer.
To determine the diameter of the throat, we use the equation:
Dt =-4 X 0.51 = 0.806 inch
Next, then, is the diverging nozzle (Fig. 702). To obtain maximum thrust, we must calculate the exit area and its diameter. These will be larger than those at the throat. Our computation begins by referring to Table 7-3.
Table 7-3 Nozzle Expansion Area Ratio
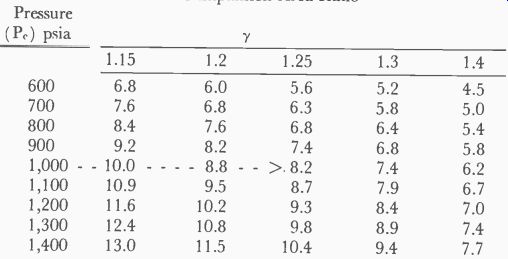
Glance down the first column P,. ( chamber pressure) to 1,000 psia.
This is the value of Pe which was given in Table 7-1. Go across that line to the column headed by a gamma of 1.25. This is also given in Table 7-1. At the intersection we find a ratio for the nozzle expansion area of 8.2.
The formula for determining the exit area, Ae, is:
A,. = 8.2 At or 8.2 times the throat area. We found the throat area to be 0.51 inch so, using the formula above, the exit area is:
0.51 X 8.2 = 4.18 sq. in.
To find the diameter of the exit end of the nozzle, we again use the formula:
We can now draw the nozzle showing the dimensions in Fig. 703.
To determine the lengths of the converging and diverging sections ...
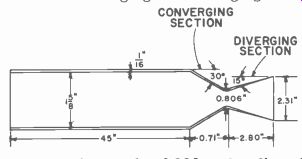
Fig. 703. Engine dimensions.
... of the nozzle we have used a converging angle of 30° and a diverging angle of 15°. We use the equations:
L. (converging length)---
0.5 (D.--Dt) tan 30° La (diverging length) =
0.5 (D.--) tan 15°
The numerical values D. and Di were found earlier.
From a set 3f trigonometric tables, tan 30° equals 0.577 and tan 15° equals 0.268.
0.5 (1.625--0.806)
0.71 in.
0.577
0.5 (2.31- 0.806) La = 2.80 in.
These are the dimensions shown in Fig. 703.
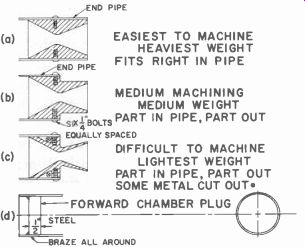
Fig. 704. Typical nozzle and plug constructions.
Now that we have completed our calculations, we find that we would use tubing 1.69 (or 1-11/16) inches 0.D., .0625 inch thick with a converging angle of 30° and a diverging angle of 15°. The nozzle will have to be machined in one of the three patterns shown in Fig. 704. Note that it is then fastened in place in the tube, with machine screws, at the right length from the plug at the other end. The plug (Fig. 704-d) should be a solid piece of 0.5-in. thick steel brazed into the tube end as shown. A rounded or bullet-shaped nose section of hardwood or metal could be fitted to this plugged end of the rocket...
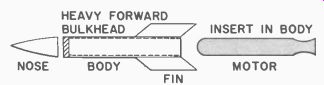
Fig. 705. Motor and body as separate units.
...motor to form an aerodynamic shape, or the rocket motor might be fitted into a rocket body as shown in Fig. 705.
Fins The tail fins may be made from 1/16-inch thick steel or 1/8-inch thick aluminum and set equidistant around the body as shown in Fig. 706. The fins can be fastened by any of several methods (some are shown in Fig. 706) but this must be done before any propellant is added.
Use special care to get the fins exactly in line with the longitudinal axis of the rocket and mounted securely so that flutter cannot cause an erratic flight. Severe flutter can cause the rocket to break up. The width of the fins from tip to tip should not be over 200 times the fin thickness. This means about 20 inches for this rocket. The length may be from 18 to 24 inches. In general, the side-view area of the rocket with fins must be larger than the front area, on each side of the center of balance, for stability in flight.
Design of a rocket motor when the tube is specified first
Before going ahead with the launching and firing, there is one additional problem in design. In this problem assume that you already have a length of steel tubing of the following dimensions:
a. Wall thickness is 1/ 16 in.
b. Outside diameter is 2 in.
c. Inside diameter is 1-7/8 in. (1.875" )
d. Length is 4 ft.
and you want to determine the thrust, the burning time of the propellant in the tube and the nozzle dimensions.
To determine the burning time, we must know the burning area and the length of the propellant in the tube. If we allot 3 inches of tube length for the nozzle and nose sections, it will leave 45 inches of the 48 for the propellant.
The area of the propellant can be calculated from:
d2 = (3.14) X (1.875)2 Area = S = 2.76 in.
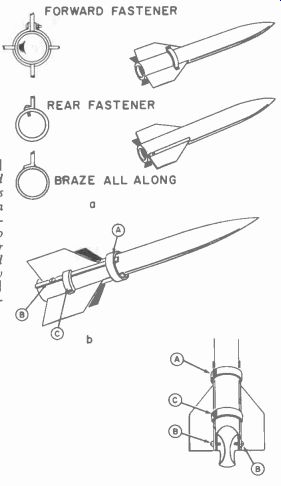
Fig. 706. Fin-assembly detail [a] and [b] "strap method" to avoid
brazing to chamber or drilling holes except those to mount nozzle. In upper
illustration [a], bolt into nozzle or motor extension but not into combustion
chamber. In lower drawing [b], ring over forward end of tail. Braze to tail
[A]. [B] Screw fasten end of tail to nozzle. [C] Braze straps between tail
fins at approximate midpoint if desired.
The weight of the propellant to be burned per second will be :
Area X burning rate X density 2.76 X 90 X 0.0932 = 23.15 lbs/sec.
The burning time of propellant in the tube will be :
Burning time (tb) = length 45= 0.5 sec.
burning rate 90 Finally, to determine how much propellant is needed by weight, multiply the weight burned per second by the burning time :
23.15 X 0.5 = 11.58 lbs of propellant.
From this we determine the weight ratios of the zinc and sulfur propellant by:
04 Zinc powder (lbs) = 2.X 11.58 = 7.77 lbs 3.04 1 Sulfur (lbs) =-
3.04 X 11.58 = 3.81 lbs Now we can compute the thrust. We will obtain, using the formula:
Thrust (F) =
Weight of propellant burned per sec. X
Exhaust velocity Gravitational constant 23.15 X 1490
= 1071 lbs of thrust 32.2
The area of the nozzle throat is determined in exactly the same manner as for our first example. Note that we must use a different row in Table 7-2 to get the thrust coefficient, 1.57.
At = 1071= 0.682 sq. in.
1.57 X 1,000 The exit area of the nozzle, again using Table 7-2, is:
A.=8.2 X At = 5.59 sq. in.
The throat and exit diameters are then calculated as before:
Dt = \I 4 X 0.628 = 0.894 in.
3.14 De = 4 4 X 5.59- 2.66 in.
3.14
Finally, to determine the lengths of the converging and diverging nozzle sections :
Le-
0.5 (1.875- 0.894)
0.85 in.
0.577 L,,=0.5 (2.66 0.894) 3.29 in.
0.268
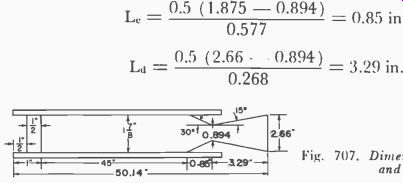
Fig. 707. Dimensions of chamber and nozzle.
We use exactly the same procedure as in the previous example with the same converging and diverging angles. It is suggested that on all nozzles the computed lengths be increased slightly so that the throat can be rounded. Do not make the lengths shorter. Rounding of the throat will add perhaps one-half inch to the length. Fig. 707 shows the dimensions of the rocket engine based on these computations.
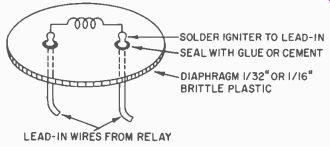
Fig. 708. Typical igniter.---- SOLDER IGNITER TO LEAD-IN SEAL WITH GLUE OR
CEMENT DIAPHRAGM I/32"OR 1/16" BRITTLE PLASTIC ; LEAD-IN WIRES FROM
RELAY
Again we have shown a 0.5-inch plug at the forward end which must be brazed in place.
Ignition systems and launchers
There is only one safe, approved method of firing a rocket and that is by electricity. This allows the person firing the rocket to remain at a safe distance from the rocket launcher when the rocket is ignited. The principle of electrical ignition is not complex. A small piece of nichrome wire is heated by passing a large electrical current through it. It will heat to incandescence. This wire is mounted on a plastic or wooden plug (Fig. 708) just large enough to fit into the nozzle end of the rocket and press against the propellant until the exhaust gases blow it out.
A relay system is necessary to pass a large current through the igniter wire (it must have short leads to it) and also to make remote operation of the igniter possible. This relay system with its battery, warning light and safety switch is the rocket ignition system. The relay can operate with a small current so we can run long wires to the ignition system from a distant bunker and fire our rocket motor from a safe position.
Always keep a short circuit across the igniter until the last moment before you are ready to fire the rocket. Never connect the igniter to the ignition system until the last moment before firing.
In the ignition system circuit shown in Fig. 709, starting at the right of the diagram, note that the leads of the igniter are connected through heavy wires to a switch (S) which is shorting the line to the igniter. This is a safety short circuit. When we are ready to fire the rocket, the switch is moved down to position 2 so that the lower side of the line connects directly to the negative terminal of the 12-volt battery. The battery must be large enough to supply the heavy current required for good ignition.
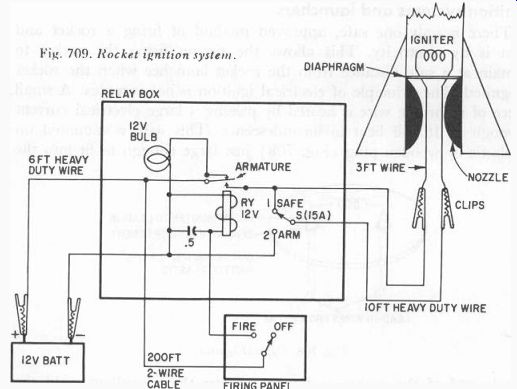
Fig. 709. Rocket ignition system.
The left wire from the igniter connects to the normally open relay contact. The relay is shown in the de-energized position. The armature of the relay is connected to the positive terminal of the 12-volt battery. The normally closed relay contact is connected to the positive terminal of the battery when the armature is de-energized and the warning light is connected to this contact. This will always indicate that the battery has been connected to ignition system. Be careful when this light burns! The relay has a 0.5 uf capacitor across its windings. This causes a delay in the releasing action of the relay to insure ignition even though the firing button is depressed only momentarily.
Blast-off techniques
When the rocket is ready to fire the last person to leave the launching area will manually change the position of the safe-arm switch (S) to the arm position. This same person should be the only one who is authorized to depress the firing switch back at the bunker.
After closing the firing switch on the firing panel the rocket should blast off. If it does not, try three more times at five-minute intervals (if the battery is weak this will allow it to recover somewhat to give another current jolt to the igniter). If the rocket still does not fire, wait at least 30 minutes before anyone approaches it; then one person goes to the launcher and, first, moves the safe-arm switch to safe; next, disconnects the igniter wires; last, removes the igniter.
Check that:
a. Firing switch is off
b. Safety switch is at safe
c. Rocket igniter wires arc shorted (wrapped together) A typical rocket launching count down or operations procedure is as follows:
17. Place rocket on launcher. Send all extra persons from rocket launch area.
16. Place relay box (ignition system) 10 feet from launcher.
15. Connect battery to ignition system.
14. Check that safety light is on.
13. Connect the firing panel to the ignition system.
12. Connect an extra igniter to the ignition system leads. Do not put this igniter in the rocket.
11. Place safe-arm switch to arm.
10. Operate the fire switch.
9. Check to see if the test igniter has burned through. This is a test of the firing circuit. If the igniter has burned through, go ahead with the next step.
If not, check the firing system till it operates satisfactorily.
8. Turn fire switch off.
7. Place the safe-arm switch to safe.
6. Send all personnel but one from the launcher area.
Other personnel should be at least 200 feet away and under cover.
5. Place the rocket igniter inside the rocket nozzle up against the propellant and un-short the leads.
4. Attach the relay box leads to the rocket igniter.
3. Place the safe-arm switch to arm.
2. The last man now goes to the safe area which is 200 feet away.
He gets under protective cover.
1. This last man operates the fire switch.
BLAST-OFF !

Fig. 710. Early model of Nike Zeus.
When rocket is away, turn firing-control switch off. Wait to be sure the rocket has impacted before leaving shelter.
The rocket launcher
We have discussed the firing procedure and launching but as yet have not discussed the actual types of launchers which can be used with small rockets. Fig. 710 shows an early model of the Nike Zeus.
Note the structural strength and rigidity built into its launching arm.
Fig. 711 shows a Nike Hercules and in the almost vertically erect position a Nike Ajax. All three of these missiles are held in place on their launchers by a small clip or finger in such a way that they can be elevated or depressed, yet, when fired, a few inches of movement frees them from the launcher rail.
We can say that the rocket launcher has two purposes:
a. To support the rocket till it is launched.
b. To provide initial direction in guidance.

Fig. 711. Nike Hercules [left] and Nike Ajax.
There are three launching methods which are suitable.
These are:
a. The Ring over Pole.
b. The Clip on Rail.
c. The Slotted Rail.
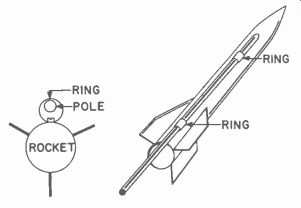
Fig. 712. Ring over Pole.
The three types are illustrated in Figs. 712, 713, 714.
The Ring-over-Pole type requires that the pole be securely fastened in a solid mounting base and be stiff enough to avoid bending or
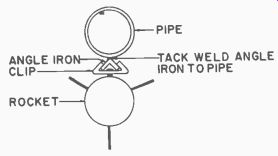
Fig. 713. cup on Rail.
whipping. A 3/4-inch steel rod and 1-inch rings on the rocket will usually be satisfactory for the size rockets we have discussed. Normally, the' pole is inclined about 5° from the vertical, and should be solidly set in a concrete base.
The Clip-on-Rail type can be made of 1 X 1 X 1/4-inch angle iron, so arranged that the clip on the rocket body is able to grip the angle as shown in Fig. 713. The angle iron must be fastened to a piece of 2-inch pipe to get the required rigidity. This type of rail can be rein forced easily to prevent bending or whipping when the rocket is in motion.
The Slotted Rail (Fig. 714) may he constructed by welding together four pieces of 3A X 3A X Vs-inch angle iron. The standing
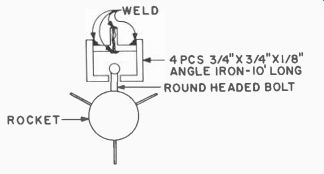
Fig. 714. Slotted Rail.
legs of two of the angles arc welded back to back, forming a channel for rigidity. The other two pieces of angle iron arc welded to the running legs of the angles to form a slotted track. A ready-made version can be obtained from a 10-foot piece of square steel door track. Two bolts with rounded heads arc screwed into the rocket body (they must not go into the propellant chamber). When the rocket is placed on the launcher it hangs from these bolts inserted in the track as shown.
The launcher base (Fig. 715) may be made from an 18-inch square of IA-inch steel plate. Drill holes in each corner to receive the steel...
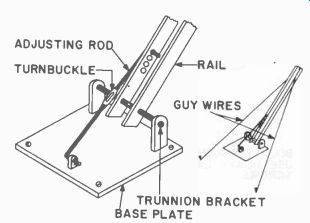
Fig. 715. Launcher base.
...hold-down stakes. A trunnion bracket is welded to the plate and the rein is fastened to the bracket by means of a bolt. The elevation angle can be adjusted by setting the adjusting rod in a suitable hole and making fine adjustments with the turnbuckle. When the launching rail is properly positioned in azimuth and elevation, the steel guy wires arc securely fastened to maintain the launcher in the correct position during the firing.
Generally the launcher is oriented in azimuth by means of a com pass and the elevation angle determined by means of a plumb bob and a protractor. Remember, you do not want an exact vertical shot.
An elevation angle of about 85° is best for high altitude attempts and an angle of about 50° is best when you arc interested in obtaining maximum range or distance.
Static testing of the rocket
For the static test we clamp the rocket engine into a fixture so that it cannot go any place. Then we fire the rocket engine to test whether it will function properly. This is a good idea when trying out a new design. Everything can be tested, the firing panel, the igniter and the rocket engine. The same care must be used as in an actual firing, and unless it is absolutely certain that there has been no weakening of or damage to the rocket engine cast because of this firing, it should not be reloaded and fired again.
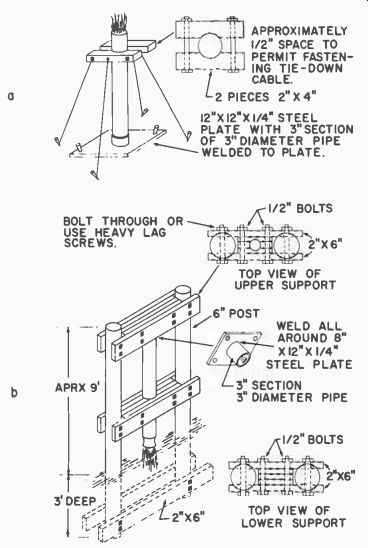
Fig. 716. Static test stands (a and b).
Two static-test stand designs arc given in Fig. 716. In the first design, the rocket nozzle is pointed up so that the rocket pushes against the base plate resting on the ground. Fig. 716-b shows how the stand might be constructed to hold the rocket while it exerts an upward thrust of 800 to 1,000 pounds. Take care to make this stand strong and rigid.
Remember, learn all you can about theory and practice. If you form a club you can share the expense and be more likely to obtain help from military and civilian rocket experts. Then you can be safely on your way to a new and exciting career in the Space Age.